早教吧作业答案频道 -->数学-->
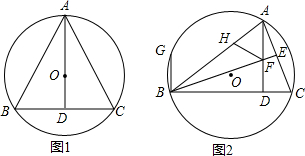
已知锐角三角形ABC内接于O,AD⊥BC.垂足为D.(1)如图1,若AB=BC,BD=DC,求∠B的度数.(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交O于点G,在AB边上取一点H,使得AH=BG;求证
题目详情
已知锐角三角形ABC内接于 O,AD⊥BC.垂足为D.
(1)如图1,若
=
,BD=DC,求∠B的度数.
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交 O于点G,在AB边上取一点H,使得AH=BG;求证:△AFH是等腰三角形.
(1)如图1,若
 |
| AB |
 |
| BC |
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交 O于点G,在AB边上取一点H,使得AH=BG;求证:△AFH是等腰三角形.

▼优质解答
答案和解析
(1)∵
=
,
∴AB=BC.
∵AD⊥BC,BD=DC,
∴AD是线段BC的垂直平分线,
∴AB=AC,
∴△ABC是等边三角形,
∴∠B=60°;
(2)连接GC,GA,
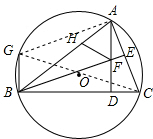 ∵BG⊥BC,
∵BG⊥BC,
∴GC是 O的直径,
∴∠GAC=90°.
∵BE⊥AC,
∴∠BEC=∠GAC=90°,
∴AG∥BE.
∵AD⊥BC,
∴∠ADC=∠GBC=90°,
∴BG∥AD,
∴四边形GBFA是平行四边形,
∴BG=AF.
∵BG=AH,
∴AH=AF,
∴△AFH是等腰三角形.
 |
| AB |
 |
| BC |
∴AB=BC.
∵AD⊥BC,BD=DC,
∴AD是线段BC的垂直平分线,
∴AB=AC,
∴△ABC是等边三角形,
∴∠B=60°;
(2)连接GC,GA,
 ∵BG⊥BC,
∵BG⊥BC,∴GC是 O的直径,
∴∠GAC=90°.
∵BE⊥AC,
∴∠BEC=∠GAC=90°,
∴AG∥BE.
∵AD⊥BC,
∴∠ADC=∠GBC=90°,
∴BG∥AD,
∴四边形GBFA是平行四边形,
∴BG=AF.
∵BG=AH,
∴AH=AF,
∴△AFH是等腰三角形.
看了 已知锐角三角形ABC内接于O...的网友还看了以下:
读下图,据此回答1-3题:1.四幅图中位在亚洲与北美洲边界的图是:A.a图B.b图C.c图D.d图 2020-05-02 …
下图所示为12月22日A、B、C、D四地昼夜长短示意图,阴影代表黑夜,据图回答1—3题。1、水平运 2020-05-02 …
如图所示,为电流及其磁场的磁感线分布图示,其中正确的是()A.图(a)和图(b)B.图(b)和图( 2020-05-02 …
如图是关于人体免疫的图解,属于保卫人体的第一道防线的图是:()A.A图和B图B.A图C.B图和D图 2020-05-02 …
读下图,回答下列各题。1.上面四幅图中,表示实际范围最大的是A.a图B.b图C.c图D.d图2.上 2020-05-02 …
若图为三圈环流中的中纬度环流侧视图,读图回答题。1.a、b、c、d四点气压由高到低排序正确的是2. 2020-08-01 …
如图是细胞分裂期的四个时期模式图,下列说法错误的是()A.动物细胞有丝分裂与该图不同之处主要表现在A 2020-11-07 …
读不同地点昼长随季节变化统计曲线图(注意a、d图中加粗部分)完成33~34题.图中a、b、c、d四地 2020-11-10 …
将图1中A、B、C、D四地气候类型与图2中甲、乙、丙、丁一一对应正确的是()A.A-甲、B-乙、C- 2020-11-30 …
2道卡诺图化简用卡诺图化简下列逻辑函数1.F(A,B,C,D)=BC’D+AB’C’D,其中C+D= 2020-12-23 …