早教吧作业答案频道 -->数学-->
四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AB=2,若该四棱锥的所有顶点都在体积为243π16同一球面上,则PA=.
题目详情
四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AB=2,若该四棱锥的所有顶点都在体积为
同一球面上,则PA=___.
| 243π |
| 16 |
▼优质解答
答案和解析
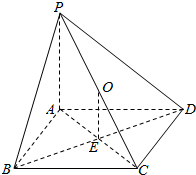 连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为
连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为
PC=
=
,
所以由球的体积可得
π(
)3=
,解得PA=
,
故答案为:
.
 连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为
连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为| 1 |
| 2 |
| 1 |
| 2 |
| PA2+AC2 |
| 1 |
| 2 |
| PA2+8 |
所以由球的体积可得
| 4 |
| 3 |
| 1 |
| 2 |
| PA2+8 |
| 243π |
| 16 |
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
看了 四棱锥P-ABCD的底面AB...的网友还看了以下:
制气体时为什么要先放固体后放液体用锥形瓶和长颈漏斗作反应容器时,为什么要先放固体后放液体?例如,用 2020-04-06 …
某兴趣小组利用下图装置进行二氧化碳的制取和部分性质实验,回答下列问题:(1)关闭E打开C,从长颈漏 2020-05-13 …
离心式分离器主要由( )等组成.A.筒体、锥形管、螺旋叶片、中心管、进口管、排污管、积液罐B.筒体、 2020-05-31 …
管钳是用来转动金属管或其他()工件,为管路安装和修理中常用工具。A.圆柱形B.球形C.方形D.锥形 2020-05-31 …
9.SO3分子构型为()A.三角锥B.平面三角形C.四面体D.V形 2020-06-04 …
下列说法不正确的是()A.长颈漏斗可以方便的添加液体B.启普发生器可以控制反应的速率C.分液漏斗可 2020-07-10 …
有下列仪器:a试管b烧杯c量筒d锥形瓶e集气瓶f试剂瓶g玻璃棒h胶头滴管,其中(1)给液体直接加热 2020-07-15 …
在对陆地生活动物的叙述中,不正确的是()A.穴居的动物身体呈锥形或线形B.在陆地生活的动物比在水中生 2020-12-11 …
在对陆地生活动物的叙述中,不正确的是()A.穴居的动物身体呈锥形或线形B.在陆地生活的动物比在水中生 2020-12-23 …
方锥形的体积怎么求就是四个三角形组成的一个立体的锥形,和金字塔一样的形状,体积怎么算?宽1.5,长1 2020-12-25 …