如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限．其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm（1）若OB=6cm

Question

如图，平面直角坐标系中，将含 30° 的三角尺的直角顶点 C 落在第二象限．其斜边两端点 A 、 B 分别落在 x 轴、 y 轴上，且 AB =12 cm

（ 1 ）若 OB =6 cm ．

① 求点 C 的坐标；

② 若点 A 向右滑动的距离与点 B 向上滑动的距离相等，求滑动的距离；

（ 2 ）点 C 与点 O 的距离的最大值 . 

 

Answer 1

（ 1 ） ① 过点 C 作 y 轴的垂线，垂足 为 D ，如图 1 ：

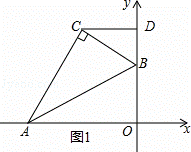
在 Rt △ AOB 中， AB =12 ， OB =6 ，则 BC =6 ，

∴∠ BAO =30° ， ∠ ABO =60° ，

又 ∵∠ CBA =60° ， ∴∠ CBD =60° ， ∠ BCD =30° ，

∴ BD =3 ， CD =3 ，

所以点 C 的坐标为（﹣ 3 ， 9 ）； -------------------------------2 分                     

② 设点 A 向右滑动的距离为 x ，根据题意得点 B 向上滑动的距离也为 x ，如图 2 ：

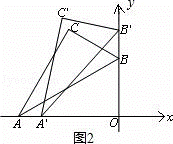
AO =12× cos ∠ BAO =12× cos 30°=6 ．

∴ A ' O =6 ﹣ x ， B ' O =6+ x ， A ' B '= AB =12

在 △ A ' O B ' 中 ， 由勾股定理得 ，

（ 6 ﹣ x ） ² + （ 6+ x ） ² =12 ² ， 解得 ： x =6 （ ﹣ 1 ），

∴ 滑动的距离为 6 （ ﹣ 1 ）； ----------------------------------------4 分

（ 2 ）设点 C 的坐标为（ x ， y ），过 C 作 CE ⊥ x 轴， CD ⊥ y 轴，垂足分别为 E ， D ，如图 3 ：

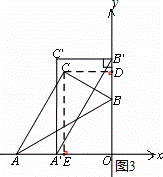
则 OE = ﹣ x ， OD = y ，

∵∠ ACE + ∠ BCE =90° ， ∠ DCB + ∠ BCE =90° ，

∴∠ ACE = ∠ DCB ，又 ∵∠ AEC = ∠ BDC =90° ，

∴△ ACE ∽△ BCD ，

∴ ，即 ，

∴ y = ﹣ x ，

OC ² = x ² + y ² = x ² + （﹣ x ） ² =4 x ² ， ------------------------------6 分

∴ 当 | x | 取最大值时，即 C 到 y 轴距离最大时， OC ² 有最大值，即 OC 取最大值，如图，即当 C ' B ' 旋转到与 y 轴垂直时

．此时 OC =12 ，

故答案为： 12