早教吧作业答案频道 -->数学-->
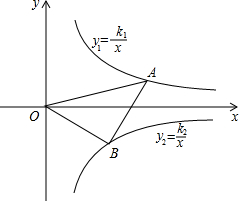
如图,在平面直角坐标系中,反比例函数y1=k1x(x>0)的图象与y2=k2x(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=k1x(x&
题目详情
如图,在平面直角坐标系中,反比例函数y1=
(x>0)的图象与y2=
(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=
(x>0)和y2=
(x>0)的图象上.若OB=AB,点B的纵坐标为-2,则点A的坐标为___.
| k1 |
| x |
| k2 |
| x |
| k1 |
| x |
| k2 |
| x |

▼优质解答
答案和解析
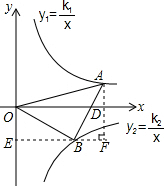 过点B作x轴的平行线EB,过点A作AF⊥EB的延长线于点F,
过点B作x轴的平行线EB,过点A作AF⊥EB的延长线于点F,
∵等腰Rt△OAB,∠OBA=90°,
∴∠OBE+∠ABF=90°,∠ABF+∠BAF=90°,
∴∠OBE=∠BAF,
在△OEB和△BFA中,
,
∴△OEB≌△BFA(AAS),
∴EO=BF=2,BE=AF,
∵设AD=y,则OE=BF=2-y,EF=2-y+2=4-y,
故A(4-y,y),B(2,y-2),
∵反比例函数y1=
(x>0)的图象与反比例函数y2=
(x>0)的图象关于x轴对称,
∴k1+k2=0,
即(4-y)y+2(y-2)=0,
解得:y1=3+
(不合题意舍去),y2=3-
,
则点A的纵坐标为:3-
,
∵EF=4-y=1+
,
∴A(1+
,3-
).
故答案为:(1+
,3-
).
 过点B作x轴的平行线EB,过点A作AF⊥EB的延长线于点F,
过点B作x轴的平行线EB,过点A作AF⊥EB的延长线于点F,∵等腰Rt△OAB,∠OBA=90°,
∴∠OBE+∠ABF=90°,∠ABF+∠BAF=90°,
∴∠OBE=∠BAF,
在△OEB和△BFA中,
|
∴△OEB≌△BFA(AAS),
∴EO=BF=2,BE=AF,
∵设AD=y,则OE=BF=2-y,EF=2-y+2=4-y,
故A(4-y,y),B(2,y-2),
∵反比例函数y1=
| k1 |
| x |
| k2 |
| x |
∴k1+k2=0,
即(4-y)y+2(y-2)=0,
解得:y1=3+
| 5 |
| 5 |
则点A的纵坐标为:3-
| 5 |
∵EF=4-y=1+
| 5 |
∴A(1+
| 5 |
| 5 |
故答案为:(1+
| 5 |
| 5 |
看了 如图,在平面直角坐标系中,反...的网友还看了以下:
谁帮我仿照句子造个例句是天上的明星现了,好像点着无数的街灯.用牵牛花开放了,好象笼中的小鹦鹉,好象 2020-04-27 …
英语加音现象举例英语中经常出现加音的现象,例如像doit的中间有一个w的音;seeit的中间有一个 2020-05-14 …
例子:一个个逗号,(像象)一个个小蝌蚪.一个个省略号,(像象)(例子:一个个逗号,(像象)一个个小 2020-06-07 …
请问一下有谁能举例分析日常生活中可见的博弈现象,可以是囚徒困境、智猪博弈等模型博弈,但是必须举出现 2020-07-02 …
为什么世界上多数语言的r都发类似“了“的音?似乎只有普通话中的r和美国英语中的r是例外.多数语言的 2020-07-04 …
举出具体例子,说明生产相对过剩的经济危机和金融危机是资本主义特有的现象例子就以西方20世纪30年代 2020-07-06 …
谁最会描绘大象.例,大象的身子象像堵墙.再写4个. 2020-11-24 …
光的洐射现象例子高中,光的色散,洐射,干射现象的实例!越多越好!谢谢了! 2020-11-28 …
24字母的想象和事物的想象24字母的想象(例如):A是一座金字塔,是进取;B是两个联结在一起的心,是 2020-12-07 …
怎么根据方程画函数图象例如:y=3x+4,这么怎么画出图象,还有怎么根据图象写出方程 2021-01-15 …