早教吧作业答案频道 -->数学-->
在平面直角坐标系中,抛物线y=-12x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.(1)求抛物线的解析式;(2)在AC上方的抛物线上有一动点P.①如图1,当点P运动到某位置时
题目详情
在平面直角坐标系中,抛物线y=-
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
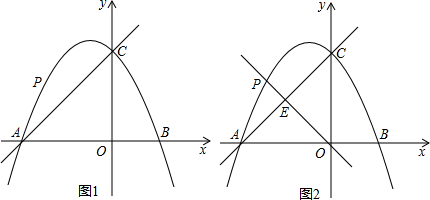
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
| 1 |
| 2 |
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.

▼优质解答
答案和解析
(1)∵直线y=x+4经过A,C两点,
∴A点坐标是(-4,0),点C坐标是(0,4),
又∵抛物线过A,C两点,
∴
,解得:
,
∴抛物线的解析式为y=-
x2-x+4.
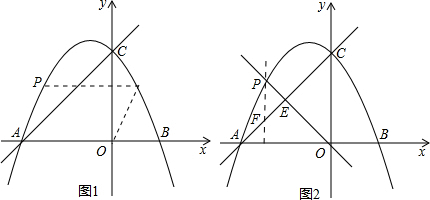
(2)①如图1
∵y=-
x2-x+4,
∴抛物线的对称轴是直线x=-1.
∵以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,
∴PQ∥AO,PQ=AO=4.
∵P,Q都在抛物线上,
∴P,Q关于直线x=-1对称,
∴P点的横坐标是-3,
∴当x=-3时,y=-
×(-3)2-(-3)+4=
,
∴P点的坐标是(-3,
);
②过P点作PF∥OC交AC于点F,
∵PF∥OC,
∴△PEF∽△OEC,
∴
=
.
又∵
=
,OC=4,
∴PF=
,
设点F(x,x+4),
∴(-
x2-x+4)-(x+4)=
,
化简得:x2+4x+3=0,解得:x1=-1,x2=-3.
当x=-1时,y=
;当x=-3时,y=
,
即P点坐标是(-1,
)或(-3,
).
又∵点P在直线y=kx上,
∴k=-
或k=-
.
∴A点坐标是(-4,0),点C坐标是(0,4),
又∵抛物线过A,C两点,
∴
|
|
∴抛物线的解析式为y=-
| 1 |
| 2 |
(2)①如图1
∵y=-
| 1 |
| 2 |
∴抛物线的对称轴是直线x=-1.
∵以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,
∴PQ∥AO,PQ=AO=4.
∵P,Q都在抛物线上,
∴P,Q关于直线x=-1对称,
∴P点的横坐标是-3,
∴当x=-3时,y=-
| 1 |
| 2 |
| 5 |
| 2 |

∴P点的坐标是(-3,
| 5 |
| 2 |
②过P点作PF∥OC交AC于点F,
∵PF∥OC,
∴△PEF∽△OEC,
∴
| PE |
| OE |
| PF |
| OC |
又∵
| PE |
| OE |
| 3 |
| 8 |
∴PF=
| 3 |
| 2 |
设点F(x,x+4),
∴(-
| 1 |
| 2 |
| 3 |
| 2 |
化简得:x2+4x+3=0,解得:x1=-1,x2=-3.
当x=-1时,y=
| 9 |
| 2 |
| 5 |
| 2 |
即P点坐标是(-1,
| 9 |
| 2 |
| 5 |
| 2 |
又∵点P在直线y=kx上,
∴k=-
| 9 |
| 2 |
| 5 |
| 6 |
看了 在平面直角坐标系中,抛物线y...的网友还看了以下:
某种动物繁殖量y(只)与时间x(年)的关系为y=log3(x+1),设这种动物第2年有100只,到 2020-05-17 …
下面以捕食关系构成的食物链是()A.哺乳动物→跳蚤→原生动物→过滤性病毒B.动植物残体→微生物→土 2020-07-03 …
某振动系统的固有频率为fo,在周期性驱动力的作用下做受迫振动,驱动力的频率为f.若驱动力的振幅保持 2020-07-11 …
、、第2题质点系的内力可以改变A、系统的总质量B、系统的总动量C、系统的总动能D、系统的总角动量第 2020-07-14 …
下列关于种间关系的描述,正确的是()A.两种生物所需的资源和占有的空间越相似,它们之间的竞争就越激烈 2020-11-25 …
某振动系统的固有频率为f0,在周期性驱动力的作用下做受迫振动,驱动力的频率为f,下列说法正确的是() 2020-11-27 …
人们经常用“自相残杀”来说明某种动物之间的关系.这种关系说的是()A.互助关系B.斗争关系C.配偶关 2020-12-01 …
下列社会关系不属于劳动法调整对象的是:A作者与出版社之间的关系B某私营企业与职工因支付加班费用问题而 2020-12-01 …
关于生态系统中信息传递及其应用的叙述,正确的是()A.生态系统中植物都是通过化学物质传递信息B.生态 2020-12-15 …
下列关于人体代谢和调节的叙述正确的是()A.切断小鼠大脑皮层与下丘脑的神经联系,小鼠不能维持体温恒定 2020-12-22 …