公元263年左右,我国数学家刘徽发现当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了割圆术。利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14
公元263年左右,我国数学家刘徽发现当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了割圆术。利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率。如图是利用刘徽的割圆术设计的程序框图,则输出的n值为(参考数据:![]() =1.732,
=1.732,![]() )
)
A 12 B 24 C 36 D48
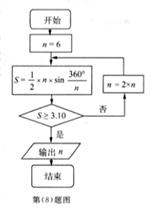
B
【解析】n=6,s=![]()
![]() 2.598
2.598
n=12,s=3
n=24,s=3.1056![]() 结束循环
结束循环
输出n=24
英语翻译如果正在做的项目有后续追加.最低就不是25元了.(我的意思想表达,如果是小项目呢,就不按天 2020-04-09 …
∫f(x-t)dt上限是x,下限是0用u=x-t换元后为什么结果是∫f(u)du上限是x,下限是0 2020-05-23 …
“十•一”期间,小明一家开车外出旅游,途中看到如图所示的限速牌.小明用了10min的时间通过了这段 2020-06-02 …
怎么少了一元钱?这里用甲乙丙丁了.甲乙丙三人一人出10元,给丁,丁花了25元丢了2元然后剩下3元分 2020-06-07 …
3乘9=27+2=29元还有一元了?三个客人去旅馆住宿,住宿费30元,旅馆优惠只收了25元,便要服 2020-07-08 …
向爸爸借了500元又向妈妈借了500元了买了一双鞋子970元,剩30元还给妈妈10元,还给爸爸10 2020-07-09 …
1、师傅和徒弟加工零件,比是5:3,师傅加工了245个,徒弟比师傅少加工多少个?2、新建一所小学, 2020-07-19 …
微积分的问题我在书上看到:由有限个元素构成的集合,称为有限集合.列如:1,2,3;由无限多个元素构 2020-08-01 …
集合看不懂,书上是这样说的集合可以根据塔含有元素的个数分为两类.还有有限个元素的集合,叫有限集,集 2020-08-01 …
元代加强了对疆域的有限管理,其中管辖琉球的机构是A.江浙行省B.宣政院C.中书省D.澎湖巡检司 2020-12-24 …