早教吧作业答案频道 -->数学-->
如图,二次函数y=-x2+nx+n2-9(n为常数)的图象经过坐标原点和x轴上另一点A,顶点在第一象限.(1)求n的值和点A坐标;(2)已知一次函数y=-2x+b(b>0)分别交x轴、y轴于M、N两点.点P是二
题目详情
如图,二次函数y=-x2+nx+n2-9(n为常数)的图象经过坐标原点和x轴上另一点A,顶点在第一象限.
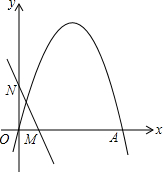
(1)求n的值和点A坐标;
(2)已知一次函数y=-2x+b(b>0)分别交x轴、y轴于M、N两点.点P是二次函数图象的y轴右侧部分上的一个动点,若PN⊥NM于N点,且△PMN与△OMN相似,求点P坐标.
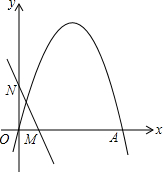
(1)求n的值和点A坐标;
(2)已知一次函数y=-2x+b(b>0)分别交x轴、y轴于M、N两点.点P是二次函数图象的y轴右侧部分上的一个动点,若PN⊥NM于N点,且△PMN与△OMN相似,求点P坐标.
▼优质解答
答案和解析
(1)∵二次函数y=-x2+nx+n2-9(n为常数)的图象经过坐标原点,
∴0=-02+n×0+n2-9.
即n2-9=0.
解得,n1=-3,n2=3.
∵二次函数y=-x2+nx+n2-9的顶点在第一象限,-1<0,
∴n>0,
∴n=3.
∴二次函数y=-x2+3x.
令0=-x2+3x,得x1=0,x2=3.
∴二次函数y=-x2+3x与x轴的交点为(0,0)或(3,0).
∵二次函数y=-x2+nx+n2-9(n为常数)的图象经过坐标原点和x轴上另一点A,
∴点A的坐标为(3,0).
由上可得,n=3,点A的坐标为(3,0).
(2)过点P作PB⊥y轴于点B,设点P的坐标为(x,-x2+3x).
∵PN⊥NM,∠NOM=90°,
∴要使△PMN与△MNO相似,
则分两种情况:
第一种情况:△PMN∽△MNO,如下图,
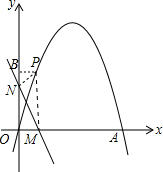
∵一次函数y=-2x+b(b>0)分别交x轴、y轴于M、N两点,
∴OM=
b,ON=b,
∴
=
.
又∵△PMN∽△NMO,
∴
=
=
.
∵PN⊥MN,PB⊥y轴,
∴△PNB∽△MNO.
∴
=
=
.
解得,x1=
,x2=0(舍去).
∴点P的坐标为:(
,
).
第二种情况:△PMN∽△NMO,如下图,
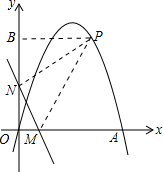
∵一次函数y=-2x+b(b>0)分别交x轴、y轴于M、N两点,
∴OM=
b,ON=b,
∴
=
.
又∵△PMN∽△NMO,
∴
=
=
.
∵PN⊥MN,PB⊥y轴,
∴△PNB∽△NMO.
∴
=
=2.
解得,x1=2,x2=0(舍去).
∴点P的坐标为(2,2).
由上可得,点P的坐标为:(
,
)或(2,2).
∴0=-02+n×0+n2-9.
即n2-9=0.
解得,n1=-3,n2=3.
∵二次函数y=-x2+nx+n2-9的顶点在第一象限,-1<0,
∴n>0,
∴n=3.
∴二次函数y=-x2+3x.
令0=-x2+3x,得x1=0,x2=3.
∴二次函数y=-x2+3x与x轴的交点为(0,0)或(3,0).
∵二次函数y=-x2+nx+n2-9(n为常数)的图象经过坐标原点和x轴上另一点A,
∴点A的坐标为(3,0).
由上可得,n=3,点A的坐标为(3,0).
(2)过点P作PB⊥y轴于点B,设点P的坐标为(x,-x2+3x).
∵PN⊥NM,∠NOM=90°,
∴要使△PMN与△MNO相似,
则分两种情况:
第一种情况:△PMN∽△MNO,如下图,
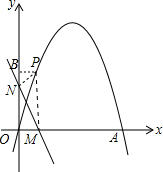
∵一次函数y=-2x+b(b>0)分别交x轴、y轴于M、N两点,
∴OM=
| 1 |
| 2 |
∴
| OM |
| ON |
| 1 |
| 2 |
又∵△PMN∽△NMO,
∴
| PN |
| MN |
| MO |
| NO |
| 1 |
| 2 |
∵PN⊥MN,PB⊥y轴,
∴△PNB∽△MNO.
∴
| x |
| b |
| -x2+3x-b | ||
|
| 1 |
| 2 |
解得,x1=
| 1 |
| 2 |
∴点P的坐标为:(
| 1 |
| 2 |
| 5 |
| 4 |
第二种情况:△PMN∽△NMO,如下图,

∵一次函数y=-2x+b(b>0)分别交x轴、y轴于M、N两点,
∴OM=
| 1 |
| 2 |
∴
| OM |
| ON |
| 1 |
| 2 |
又∵△PMN∽△NMO,
∴
| PN |
| MN |
| NO |
| MO |
| 2 |
| 1 |
∵PN⊥MN,PB⊥y轴,
∴△PNB∽△NMO.
∴
| x |
| b |
| -x2+3x-b | ||
|
解得,x1=2,x2=0(舍去).
∴点P的坐标为(2,2).
由上可得,点P的坐标为:(
| 1 |
| 2 |
| 5 |
| 4 |
看了 如图,二次函数y=-x2+n...的网友还看了以下:
已知一次函数y=kx+b(b≠0)(1)若此一次函数y=kx+b的图像与函数y=-x+b的图像关于 2020-04-08 …
一次函数y=x+1图像是直线L,与反比例函数y=k1/x图像一次函数Y=X+1的图像是直线L,与反 2020-04-08 …
如图,直线AB是一次函数y=x+a的图象,直线AC是一次函数y=-2x+b的图象,(b》a》0), 2020-05-13 …
如图,已知一次函数y=kx+b的图像与反比例函数y=8/x的图像交于A,B如图所示,已知一次函数y 2020-06-14 …
如图,一次函数y=kx+b的图像与反比例函数y=m/x的图像交于A,B两点 (1)利用图像中的条件 2020-06-27 …
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y= 2020-07-13 …
已知一次函数y=kx+b的图象经过点P(0,-3),且与函数y=1/2x+1的图象交与点A(8/3 2020-07-20 …
如图,反比例函数y=kx与一次函数y=ax+b的图象交于点A(2,2)、B(12,n).(1)求这 2020-08-03 …
如图已知函数y=-1/2x+b的图像与x轴y轴分别交于点A、B与函数y=x的图像交于点M点M的如图已 2020-12-12 …
如图,在平面直角坐标系中,一次函数y=kx=b的图像与反比例函数y=x分之n的图像交与点已知:如图, 2021-01-10 …