早教吧作业答案频道 -->数学-->
如图,在平行四边形ABCD中,∠BAD=45°.分别以BC、CD为边向外作△BCF和△DCE,使BF=BC,DE=DC,∠FBC=∠CDE,延长AB交边FC于点H,点H在F、C两点之间,连结AE、AF、DF.(1)求证:△ABF≌△EDA.(2
题目详情
如图,在平行四边形ABCD中,∠BAD=45°.分别以BC、CD为边向外作△BCF和△DCE,使BF=BC,DE=DC,∠FBC=∠CDE,延长AB交边FC于点H,点H在F、C两点之间,连结AE、AF、DF.
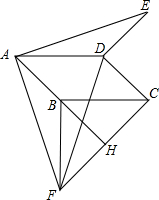
(1)求证:△ABF≌△EDA.
(2)当AE⊥AF时,求∠FBH的度数.
(3)在(2)的条件下,若B为AH的中点,求sin∠ADF的值.

(1)求证:△ABF≌△EDA.
(2)当AE⊥AF时,求∠FBH的度数.
(3)在(2)的条件下,若B为AH的中点,求sin∠ADF的值.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠ABC=∠ADC,
∵BF=BC,DE=DC,∠FBC=∠CDE,
∴AB=ED,FB=AD,∠ABF=∠EDA,
在△ABF和△EDA中,
,
∴△ABF≌△EDA(SAS);
(2)∵△ABF≌△EDA,
∴∠AFB=∠DAE,
∵AE⊥AF,∠BAD=45°,
∴∠FAB+∠DAE=90°-∠BAD=45°,
∴∠FBH=∠FAB+∠AFB=∠FAB+∠DAE=45°;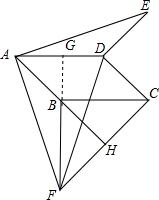
(3)∵△ABF≌△EDA,
∴AD=BF,DE=AB,
∵BF=BC,DE=DC,
∴AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBH=∠BAD=45°,
∴∠FBC=90°,
延长FB交AD于G,
∴∠DGB=∠FBC=90°,
∴△ABG与△BHF是等腰直角三角形,
设AG=BG=x,
∴AB=BH=
x,
∴BF=AD=2x,
∴DG=x,GF=3x,
∴DF=
x,
∴sin∠ADF=
=
=
.
∴AD=BC,AB=CD,∠ABC=∠ADC,
∵BF=BC,DE=DC,∠FBC=∠CDE,
∴AB=ED,FB=AD,∠ABF=∠EDA,
在△ABF和△EDA中,
|
∴△ABF≌△EDA(SAS);
(2)∵△ABF≌△EDA,
∴∠AFB=∠DAE,
∵AE⊥AF,∠BAD=45°,
∴∠FAB+∠DAE=90°-∠BAD=45°,
∴∠FBH=∠FAB+∠AFB=∠FAB+∠DAE=45°;

(3)∵△ABF≌△EDA,
∴AD=BF,DE=AB,
∵BF=BC,DE=DC,
∴AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBH=∠BAD=45°,
∴∠FBC=90°,
延长FB交AD于G,
∴∠DGB=∠FBC=90°,
∴△ABG与△BHF是等腰直角三角形,
设AG=BG=x,
∴AB=BH=
| 2 |
∴BF=AD=2x,
∴DG=x,GF=3x,
∴DF=
| 10 |
∴sin∠ADF=
| GF |
| DF |
| 3x | ||
|
3
| ||
| 10 |
看了 如图,在平行四边形ABCD中...的网友还看了以下:
在梯形ABCD中,AD平行于BC(AD还有一题:矩行ABCD(AB>AD,A在左下,B在右下,C在 2020-05-01 …
求解一道初三几何函数题.已知在梯形ABCD中,AD//BC,AB=DC=AD=6,∠ABC=60° 2020-05-17 …
在塔底B处测得山顶C的仰角为60,在山顶C处测得塔顶A的俯角为45,塔高AB=20m,求山高DC 2020-05-17 …
如图所示,在塔顶B测得山顶C的俯角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20m 2020-05-17 …
在等腰梯形ABCD中,∠DCB=60°,AD∥BC,且AD=DC,点E,F分别在AD,DC的延长线 2020-06-06 …
如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD= 2020-07-21 …
已知:如图19.3-16,在梯形ABCD中,AD‖BC,AB=DC,点E,F分别在AB,DC上,且 2020-07-29 …
(1)如图,a、b、c在数轴上的位置如图所示,化简:|a+b|-2|a+c|-|c-b|;(2)已 2020-07-30 …
(2012•洛阳模拟)如图,在直角梯形ABCD中,AD⊥AB,AB∥DC,AD=DC=1,AB=2, 2020-11-02 …
如图,在塔底B测得山顶C处的仰角为60度,在山顶C测得塔顶A的俯角为45度,已知塔高为AB=20m, 2020-11-20 …