如图，P是抛物线y=2（x-2）2的对称轴上一个动点，直线x=t平行于y轴，分别与直线y=x、抛物线交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，则满足条件的t值有（）A.1个B

Question

如图，P是抛物线y=2（x-2）²的对称轴上一个动点，直线x=t平行于y轴，分别与直线y=x、抛物线交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，则满足条件的t值有（　　）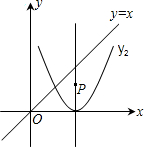

A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

∵y=2（x-2）²=2x²-8x+8，
∴对称轴为x=2，故P点横坐标为2；
当x=t时，直线y=x=t，故A（t，t）；
则y=2x²-8x+8=2t²-8t+8，故B（t，2t²-8t+8）；
若△ABP是以点A或点B为直角顶点的等腰直角三角形，则有AB=AP或AB=BP，
此时AB=|2t²-8t+8-t|，AP=|t-2|，
可得：|t-2|=|2t²-8t+8-t|；
当2t²-8t+8-t=t-2时，如图1，

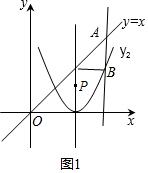
则有t²-5t+5=0，解得t₁=(5±√(5))/(2)；
当2t²-8t+8-t=2-t时，如图2，

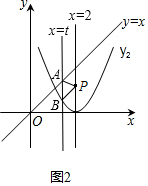
则有t²-4t+3=0，解得t₂=1，t₃=3；
故符合条件的t值为1或3或(5±√(5))/(2)共4个，
故选D．