早教吧作业答案频道 -->数学-->
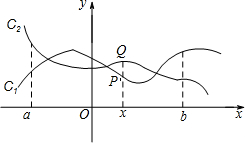
如图,点P(x,y1))与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函
题目详情
如图,点P(x,y1))与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.
(1)判断函数y=3x+2与y=2x+1在-2≤x≤0上是否为“相邻函数”,并说明理由;
(2)若函数y=
与y=-2x+a在1≤x≤2上是“相邻函数”,请求出a的最大值与最小值.
(3)若函数y=x2-(2a-1)x与y=x-2在1≤x≤2上是“相邻函数”,求a的取值范围.

(1)判断函数y=3x+2与y=2x+1在-2≤x≤0上是否为“相邻函数”,并说明理由;
(2)若函数y=
| 2 |
| x |
(3)若函数y=x2-(2a-1)x与y=x-2在1≤x≤2上是“相邻函数”,求a的取值范围.
▼优质解答
答案和解析
(1)是“相邻函数”.
理由如下:
y1-y2=(3x+2)-(2x+1)=x+1,构造函数y=x+1.
∵y=x+1在-2≤x≤0上随着x的增大而增大,
∴当x=0时,函数有最大值1,当x=-2时,函数有最小值-1,即-1≤y≤1.
∴-1≤y1-y2≤1.
即函数y=3x+2与y=2x+1在-2≤x≤0上是“相邻函数”;
(2)反比例函数y=
在1≤x≤2上是减函数,
当x=1时,y1=2;当x=2时,y1=1,
当x=1时,y2=-2+a;当x=2时,y2=-4+a.
∵-1≤y1-y2≤1,
∴有
,
解得:4≤a≤5.
∴若函数y=
与y=-2x+a在1≤x≤2上是“相邻函数”,a的最大值为5,最小值为4;
(3)y1-y2=[x2-(2a-1)x]-(x-2)=x2-2ax+2=(x-a)2+2-a2.
∵y=x2-(2a-1)x与y=x-2在1≤x≤2上是“相邻函数”,
∴|y1-y2|≤1.
由二次函数的性质可知:
当x=1时,y1-y2有最大值3-2a,
当x=a时,y1-y2有最小值2-a2.
∴
,
解得:
≤a≤
.
理由如下:
y1-y2=(3x+2)-(2x+1)=x+1,构造函数y=x+1.
∵y=x+1在-2≤x≤0上随着x的增大而增大,
∴当x=0时,函数有最大值1,当x=-2时,函数有最小值-1,即-1≤y≤1.
∴-1≤y1-y2≤1.
即函数y=3x+2与y=2x+1在-2≤x≤0上是“相邻函数”;
(2)反比例函数y=
| 2 |
| x |
当x=1时,y1=2;当x=2时,y1=1,
当x=1时,y2=-2+a;当x=2时,y2=-4+a.
∵-1≤y1-y2≤1,
∴有
|
解得:4≤a≤5.
∴若函数y=
| 2 |
| x |
(3)y1-y2=[x2-(2a-1)x]-(x-2)=x2-2ax+2=(x-a)2+2-a2.
∵y=x2-(2a-1)x与y=x-2在1≤x≤2上是“相邻函数”,
∴|y1-y2|≤1.
由二次函数的性质可知:
当x=1时,y1-y2有最大值3-2a,
当x=a时,y1-y2有最小值2-a2.
∴
|
解得:
| 5 |
| 4 |
| 3 |
看了 如图,点P(x,y1))与Q...的网友还看了以下:
求一篇英语作文,高中生在假期该不该做家务,一百词观点1有些学生认为学习重要,做家务是浪费时间,观点2 2020-03-30 …
已知双曲线x^2-y^2/3=1,若一椭圆与该双曲线共焦点,且有一交点P(2,3)已知双曲线x^2 2020-04-08 …
双曲线中的中点弦问题已知双曲线C:2x^2-y^2=2与点P(1,2).1)求过P(1,2)的直线 2020-05-23 …
求拐点的个数.曲线y=(x-1)^2(x-3)^2的拐点的个数为2个.书上给出的解释因本题的曲线是 2020-06-30 …
在给定的圆周上有100个点.任取一点标上1;按顺时针方向从标有1的点往后数2个点,标上2;从标有2 2020-07-10 …
不交作业怎么惩罚我们语文老师问的不交语文作业的有如下要求:1.有创意,符合语文学科的特点2.有意义 2020-07-11 …
1.在一棵二叉树中,度为1的结点有30个,度为2的结点有32个,则该二叉树共有个结点.2.在一个容 2020-07-18 …
已知双曲线C:2x^2-y^2=2与点P(1,2)1,求过P(1,2)点的直线l的斜率取值范围,使 2020-07-24 …
1.平面内有8个点.(1)以其中每2个点为端点的线段共有多少条?(2)以其中每2个点为端点的有1. 2020-07-30 …
1比较减1期的中期和减2期中期,有什么相同点有什么不同点?2比较减1期的后期和减2期的后期,有什么相 2020-11-06 …