早教吧作业答案频道 -->数学-->
在一节数学实践课上,老师出示了这样一道题,如图1,在锐角三角形ABC中,∠A、∠B、∠C所对边分别是a、b、c,请用a、c、∠B表示b2.经过同学们的思考后,甲同学说:要将锐角三角形转化
题目详情
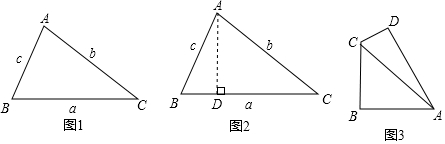
在一节数学实践课上,老师出示了这样一道题,如图1,在锐角三角形ABC中,∠A、∠B、∠C所对边分别是a、b、c,请用a、c、∠B表示b2.
经过同学们的思考后,
甲同学说:要将锐角三角形转化为直角三角形来解决,并且不能破坏∠B,因此可以经过点A,作AD⊥BC于点D,如图2,大家认同;
乙同学说要想得到b2要在Rt△ABD或Rt△ACD中解决;
丙同学说那就要先求出AD=___,BD=___;(用含c,∠B的三角函数表示)
丁同学顺着他们的思路,求出b2=AD2+DC2=___(其中sin2α+cos2α=1);请利用丁同学的结论解决如下问题:
如图3,在四边形ABCD中,∠B=∠D=90°,∠BAD=60°,AB=4,AD=5.
求AC的长(补全图形,直接写出结果即可).

经过同学们的思考后,
甲同学说:要将锐角三角形转化为直角三角形来解决,并且不能破坏∠B,因此可以经过点A,作AD⊥BC于点D,如图2,大家认同;
乙同学说要想得到b2要在Rt△ABD或Rt△ACD中解决;
丙同学说那就要先求出AD=___,BD=___;(用含c,∠B的三角函数表示)
丁同学顺着他们的思路,求出b2=AD2+DC2=___(其中sin2α+cos2α=1);请利用丁同学的结论解决如下问题:
如图3,在四边形ABCD中,∠B=∠D=90°,∠BAD=60°,AB=4,AD=5.
求AC的长(补全图形,直接写出结果即可).
▼优质解答
答案和解析
∵sinB=
,cosB=
,
∴AD=AB•sinB=c•sinB,BD=AB•cosB=c•cosB,
CD=BC-BD=a-c•cosB,
则出b2=AD2+DC2═(c•sinB)2+(a-c•cosB)2
=c2sin2B+a2+c2cos2B+2ac•cosB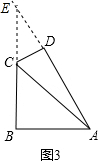
=c2(sin2B+cos2B)+a2-2ac•cosB
=a2+c2-2ac•cosB.
如图3所示,延长BC,AD交于E,
∵∠B=90°,∠BAD=60°,AB=4,
∴AE=2AB=8,∠E=30°,
∵AD=5,
∴DE=3,
∵∠ADC=∠CDE=90°,
∴CE=2
,
∴AC2=CE2+AE2-2CE•AEcos30°=12+64-2×2
×8×
=28,
∴AC=2
.
故答案是:c•sinB,c•cosB;a2+c2-2ac•cosB.
| AD |
| AB |
| BD |
| AB |
∴AD=AB•sinB=c•sinB,BD=AB•cosB=c•cosB,
CD=BC-BD=a-c•cosB,
则出b2=AD2+DC2═(c•sinB)2+(a-c•cosB)2
=c2sin2B+a2+c2cos2B+2ac•cosB

=c2(sin2B+cos2B)+a2-2ac•cosB
=a2+c2-2ac•cosB.
如图3所示,延长BC,AD交于E,
∵∠B=90°,∠BAD=60°,AB=4,
∴AE=2AB=8,∠E=30°,
∵AD=5,
∴DE=3,
∵∠ADC=∠CDE=90°,
∴CE=2
| 3 |
∴AC2=CE2+AE2-2CE•AEcos30°=12+64-2×2
| 3 |
| ||
| 2 |
∴AC=2
| 7 |
故答案是:c•sinB,c•cosB;a2+c2-2ac•cosB.
看了 在一节数学实践课上,老师出示...的网友还看了以下:
AB相距13千米,甲从A地到B,在B地停半小时后从B地回A地,乙从B地到A,在A地停留45分钟后回B 2020-03-31 …
问一个经典问题…奇数和偶数哪个多用集合思想考虑,A={奇数},B={偶数},那么在A中任何一个数都 2020-04-09 …
A=B={(x,y)/x,y∈R}f是A到B的一个映射.并满足f:(x,y)→(-xy,x-y). 2020-04-26 …
阅读下面材料:点A.B在数轴上分别表示实数a.b,A.B两点之间的距离为|AB阅读下面材料:点A. 2020-05-16 …
下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两 2020-05-16 …
已知集合A,B,若A不是B的子集,则下列命题中正确的是?A.对任意的a∈A,都有a不∈BB.对任意 2020-05-17 …
下列命题中,是假命题的是()A.在同一平面内,若a∥b,b∥c,则a∥cB.在同一平面内,若a⊥b 2020-05-17 …
为什么没有对猪弹琴,还有很多种动物可以比喻不是吗?为什么对字后面的是牛?对牛弹琴是比如A和B对话, 2020-05-22 …
力平衡状态假设AB两个物体,A在上B在下,A受力F在B上面运动,B相对地面静止,这个系统可以看作力 2020-05-22 …
三角函数题!在△ABC中,若1+cosA=(b+c)/c则三角形形状是?1.在△ABC中,若1+c 2020-05-23 …