如图1，正方形ABCD中，点P为线段BC上一个动点，若线段MN垂直AP于点E，交线段AB于M，CD于N，证明：AP=MN；如图2，正方形ABCD中，点P为线段BC上一动点，若线段MN垂直平分线段AP，分别交AB、AP、BD

Question

如图1，正方形ABCD中，点P为线段BC上一个动点，若线段MN垂直AP于点E，交线段AB于M，CD于N，证明：AP=MN；
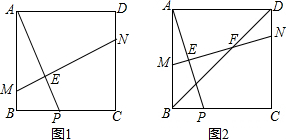
如图2，正方形ABCD中，点P为线段BC上一动点，若线段MN垂直平分线段AP，分别交AB、AP、BD、DC于点M、E、F、N．
（1）求证：EF=ME+FN；
（2）若正方形ABCD的边长为2，则线段EF的最小值=1，最大值=√(2)．

Answer 1

（1）AP=MN，
理由如下：
如图1，

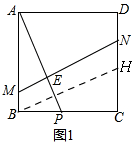
过B点作BH∥MN交CD于H，
∵BM∥NH，
∴四边形MBHN为平行四边形，
∵BH=AP，
∴MN=AP
（2）连接FA，FP，FC
∵正方形ABCD是轴对称图形，F为对角线BD上一点
∴FA=FC，
又∵FE垂直平分AP，
∴FA=FP，
∴FP=FC，
∴∠FPC=∠FCP，
∵∠FAB=∠FCP，
∴∠FAB=∠FPC，
∴∠FAB+∠FPB=180°，
∴∠ABC+∠AFP=180°，
∴∠AFP=90°，
∴FE=(1)/(2)AP，
又∵AP=MN
∴ME+EF=AP，
∴EF=ME+FN
（3）由（2）有，EF=ME+FN，
∵MN=EF+ME+NF，
∴EF=(1)/(2)MN，
∵AC，BD是正方形的对角线，
∴BD=2√(2)，
当点P和点B重合时，EF最小=(1)/(2)MN=(1)/(2)AB=1，
当点P和C重合时，EF最大=(1)/(2)MN=(1)/(2)BD=√(2)，
故答案为1，√(2)