早教吧作业答案频道 -->数学-->
如图,在△ABC中,AD,BD分别平分∠CAB和∠CBA,相交于点D.(1)如图1,过点D作DE∥AC,DF∥BC分别交AB于点E、F.①若∠EDF=80°,则∠C=;②若∠EDF=x°,证明:∠ADB=(90+x2
题目详情
如图,在△ABC中,AD,BD分别平分∠CAB和∠CBA,相交于点D.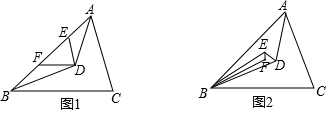
(1)如图1,过点D作DE∥AC,DF∥BC分别交AB于点E、F.
①若∠EDF=80°,则∠C=___;
②若∠EDF=x°,证明:∠ADB=(90+
)°.
(2)如图2,若DE,BE分别平分∠ADB和∠ABD,且EF,BF分别平分∠BED和∠EBD,若∠BFE的度数是整数,求∠BFE至少是多少度?
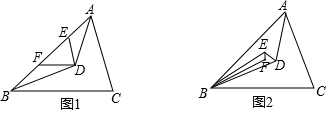
(1)如图1,过点D作DE∥AC,DF∥BC分别交AB于点E、F.
①若∠EDF=80°,则∠C=___;
②若∠EDF=x°,证明:∠ADB=(90+
| x |
| 2 |
(2)如图2,若DE,BE分别平分∠ADB和∠ABD,且EF,BF分别平分∠BED和∠EBD,若∠BFE的度数是整数,求∠BFE至少是多少度?
▼优质解答
答案和解析
(1)∵∠EDF=80°,
∴∠DEF+∠EDF=180°-80°=100°,
∵DE∥AC,
∴∠BED=∠BAC,
同理得:∠EFD=∠ABC,
∴∠ABC+∠BAC=∠DEF+∠EDF=100°,
∴∠C=80°
故答案为:80°;
②∵∠EDF=x°,
∴∠DEF+∠EFD=180°-x°,
∵DE∥AC,
∴∠BED=∠BAC,
∵AD平分∠BAC,
∴∠BAC=2∠BAD,
∴∠DEF=2∠BAD,
同理得:∠EFD=2∠ABD,
∴∠BAD+∠ABD=
,
∴∠ADB=180°-∠ABD-∠BAD=180°-
=90°+
=(90+
)°;
(2)∵DE平分∠ADB,
∴∠BDE=
∠ADB=45°+
,
∵∠BED+∠DBE=180°-∠BDE,
∵EF,BF分别平分∠BED和∠EBD,
∴
∠BED+
∠DBE=90°-
∠BDE,
即∠BEF+∠EBF=90°-
∠BDE,
∴∠BFE=180°-(∠BEF+∠EBF),
=180°-(90°-
∠BDE),
=90°+
∠BDE,
=90°+
(45°+
),
=90°+22°+
+
x,
=112°+
,
∵∠BFE的度数是整数,
当x=4时,∠BFE=113°.
答:∠BFE至少是113度.
∴∠DEF+∠EDF=180°-80°=100°,
∵DE∥AC,
∴∠BED=∠BAC,
同理得:∠EFD=∠ABC,
∴∠ABC+∠BAC=∠DEF+∠EDF=100°,
∴∠C=80°
故答案为:80°;
②∵∠EDF=x°,
∴∠DEF+∠EFD=180°-x°,
∵DE∥AC,
∴∠BED=∠BAC,
∵AD平分∠BAC,
∴∠BAC=2∠BAD,
∴∠DEF=2∠BAD,
同理得:∠EFD=2∠ABD,
∴∠BAD+∠ABD=
| 180°-x° |
| 2 |
∴∠ADB=180°-∠ABD-∠BAD=180°-
| 180°-x° |
| 2 |
| x° |
| 2 |
| x |
| 2 |
(2)∵DE平分∠ADB,
∴∠BDE=
| 1 |
| 2 |
| x |
| 4 |
∵∠BED+∠DBE=180°-∠BDE,
∵EF,BF分别平分∠BED和∠EBD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠BEF+∠EBF=90°-
| 1 |
| 2 |
∴∠BFE=180°-(∠BEF+∠EBF),
=180°-(90°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
| x |
| 4 |
=90°+22°+
| 1 |
| 2 |
| 1 |
| 8 |
=112°+
| 4+x |
| 8 |
∵∠BFE的度数是整数,
当x=4时,∠BFE=113°.
答:∠BFE至少是113度.
看了 如图,在△ABC中,AD,B...的网友还看了以下:
满足{a}⊆M⊆{a,b,c,d}的集合M的个数是( ) 是{a} {a,b} {a,c} {a, 2020-04-05 …
若非空集合M⊆N={a,b,c,d},则M的个数为8个{a},{b},{c},{d},{a,b}, 2020-05-15 …
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
A.πA,D(σC=D(R×S))B.πA,R,D(σS,C=R,D/(R×S))C.πA,R,D( 2020-05-26 …
A.πA,D(σC=D(R×S))B.πA,R.D(σR.C=S.D(R×S))C.πA,R.D(σ 2020-05-26 …
A.πA,D(σC=D(R×S))B.πA,R.D(σS.C=R.D(R×S))C.πA,R.D(σ 2020-05-26 …
如果正数a,b,c,d满足a+b=cd=4,那么()A.ab≤c+d且等号成立时a,b,c,d的取 2020-07-09 …
圆的计算题回答者+30分哦圆:r半径d直径c周长s面积r=12s=d=2.4c=c=62.8d=r 2020-07-18 …
设C,D是两个随机事件,下面哪个叙述是正确的()A.C∩D与C∪D互斥B.C∩D与C∩(D的对立事件 2020-12-01 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …