如图，已知长方形ABCD中，AD=6，AB=8，P是AD边上的点，将△ABP沿BP折叠，使点A落在点E上，PE、BE与CD分别交于点O、F，且OD=OE，则AP的长为（）A.4.8B.5C.5.2D.5.4

Question

如图，已知长方形ABCD中，AD=6，AB=8，P是AD边上的点，将△ABP沿BP折叠，使点A落在点E上，PE、BE与CD分别交于点O、F，且OD=OE，则AP的长为（　　）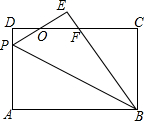

A. 4.8

B. 5

C. 5.2

D. 5.4

Answer 1

∵四边形ABCD是长方形，
∴∠A=∠C=∠D=90°，CD=AB=8，BC=AD=6，
由折叠的性质得：EP=AP，BE=AB=8，∠E=∠A=90°，
在△ODP和△OEF中，

∠D=∠E	amp;
OD=OE	amp;
∠DOP=∠EOF	amp;

，
∴△ODP≌△OEF（ASA），
∴PD=FE，OP=OF，
∴DF=EP=AP，
设AP=x，则DF=x，FE=PD=6-x，
∴CF=CD-DF=8-x，BF=BE-FE=x+2，
在Rt△BCF中，BC²+CF²=BF²，
即6²+（8-x）²=（x+2）²，
解得：x=4.8；
故选：A．