早教吧作业答案频道 -->数学-->
如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,作∠DAF=90°,且AF=AD,过点F作EF∥AD,且EF=AF,联结CF,CE.(1)求证:FC⊥BC;(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.
题目详情
如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,作∠DAF=90°,且AF=AD,过点F作EF∥AD,且EF=AF,联结CF,CE.
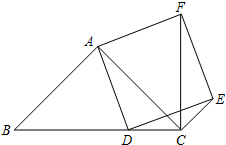
(1)求证:FC⊥BC;
(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.

(1)求证:FC⊥BC;
(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.
▼优质解答
答案和解析
(1)∵∠BAC=∠DAF=90°,
∴∠BAC-∠DAC=∠DAF-∠DAC,
即∠BAD=∠CAF,
又∵AB=AC,AD=AF,
∴△ABD≌△ACF,
∴∠B=∠ACF,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠ACF=∠B=45°,
∴∠BCF=90°,
∴FC⊥BC;
(2)∵△ABD≌△ACF,
∴BD=FC,
又∵BD=AC,
∴AC=FC,
∴∠CAF=∠CFA,
∵∠DAF=90°,EF∥AD,
∴∠DAF=∠AFE=90°,
∴∠DAC=∠EFC,
∵AD=AF,EF=AF,
∴AD=FE,
∴△ADC≌△FEC,
∴CD=CE,
∴点C在线段DE的垂直平分线上.
∴∠BAC-∠DAC=∠DAF-∠DAC,
即∠BAD=∠CAF,
又∵AB=AC,AD=AF,
∴△ABD≌△ACF,
∴∠B=∠ACF,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠ACF=∠B=45°,
∴∠BCF=90°,
∴FC⊥BC;
(2)∵△ABD≌△ACF,
∴BD=FC,
又∵BD=AC,
∴AC=FC,
∴∠CAF=∠CFA,
∵∠DAF=90°,EF∥AD,
∴∠DAF=∠AFE=90°,
∴∠DAC=∠EFC,
∵AD=AF,EF=AF,
∴AD=FE,
∴△ADC≌△FEC,
∴CD=CE,
∴点C在线段DE的垂直平分线上.
看了 如图,已知在△ABC中,∠B...的网友还看了以下:
逆转录PCR引物,在PUBMED上搜文献上找了一个引物,BLAST了一下,结果如下,但是自己不大会 2020-05-17 …
这个二阶导数题是什么意思?题目是这样的:f(x-y,y/x)=x^2-y^2,f"下标是XX,请问 2020-05-17 …
小明比小红多3个苹果,如果小明分给小红3个苹果,这时谁的苹果多?多几个?小明比小红多3个苹果,如果 2020-05-22 …
东东和妈妈去买苹果,如果买2千克,还剩下1.8元,如果买6千克则还少4.6元,他们共带了多少钱?如 2020-06-18 …
急呀求求你了赤橙黄绿青蓝紫绚烂的七彩点缀着生活试问你喜欢哪种颜色如果是红那过于热烈如果是 2020-06-24 …
.急....(要用算式,不要用方程.求求各位喇.)3.某人乘摩托车从甲地到乙地,如果每小时车速是3 2020-06-26 …
如果如图中纵轴表示某商品价格,横轴表示其互补商品需求量。下列示意图(如图)中表示某商品价格下降后其 2020-07-30 …
flex请求比如一个flex应用其中有一个写好的页面点击页面当中的按钮后处理一个事件,如果处理该事件 2020-11-21 …
三国演义读后感第6回我求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求求 2020-12-08 …
求求求求求求求求了,现等1.画展9时开门,但早有人来等候.从第一个观众来到时起,每分钟来的观众一样多 2020-12-09 …