早教吧作业答案频道 -->数学-->
如图△ABG中,∠ABG=90°,以AB为直径作O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.(1)求证:BF=GF;(2)连接BC交AG于H,若2BH=3CH,求tan∠G的值.
题目详情
如图△ABG中,∠ABG=90°,以AB为直径作 O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.
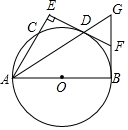
(1)求证:BF=GF;
(2)连接BC交AG于H,若2BH=3CH,求tan∠G的值.

(1)求证:BF=GF;
(2)连接BC交AG于H,若2BH=3CH,求tan∠G的值.
▼优质解答
答案和解析
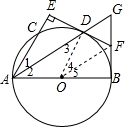 (1)∵D是弧BC的中点,
(1)∵D是弧BC的中点,
∴
=
,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠3,
∴∠1=∠3,
∴AE∥OD,
∴∠ODF=∠E=90°,
在Rt△DOF与Rt△OBF中,
,
∴Rt△DOF≌Rt△OBF,
∴∠4=∠5=
∠DOB,
∵∠DOB=∠2+∠3,
∴∠2=
∠DOB,
∴∠2=∠5,
∴AD∥OF,
∵AO=BO,
∴BF=FG;
(2)连接BD,OD交BC于P,
∵AB是 O的直径,
∴BC⊥AE,BD⊥AG,
∴BC∥EF,
∴∠5=∠DHP,
∵∠1+∠5=∠G+∠2=90°,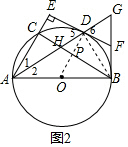
∴∠5=∠G,
∵∠5=∠6,
∴G=∠DHP,
∴BG=BH=3m,
∵△AED∽△ABG,
∴
=
=
,
∴AD:DG=5:1,
设AD=5k,DG=k,
∴BD2=AD•DG=5k2,
∴BD=
k,
∴tan∠G=
=
=
.
 (1)∵D是弧BC的中点,
(1)∵D是弧BC的中点,∴
 |
| CD |
 |
| BD |
∴∠1=∠2,
∵OA=OD,
∴∠2=∠3,
∴∠1=∠3,
∴AE∥OD,
∴∠ODF=∠E=90°,
在Rt△DOF与Rt△OBF中,
|
∴Rt△DOF≌Rt△OBF,
∴∠4=∠5=
| 1 |
| 2 |
∵∠DOB=∠2+∠3,
∴∠2=
| 1 |
| 2 |
∴∠2=∠5,
∴AD∥OF,
∵AO=BO,
∴BF=FG;
(2)连接BD,OD交BC于P,
∵AB是 O的直径,
∴BC⊥AE,BD⊥AG,
∴BC∥EF,
∴∠5=∠DHP,
∵∠1+∠5=∠G+∠2=90°,

∴∠5=∠G,
∵∠5=∠6,
∴G=∠DHP,
∴BG=BH=3m,
∵△AED∽△ABG,
∴
| AD |
| AG |
| DE |
| BG |
| 5 |
| 6 |
∴AD:DG=5:1,
设AD=5k,DG=k,
∴BD2=AD•DG=5k2,
∴BD=
| 5 |
∴tan∠G=
| BD |
| DG |
| ||
| k |
| 5 |
看了 如图△ABG中,∠ABG=9...的网友还看了以下:
高一数学圆与直线系方程过点P(2,3)引直线与圆x^2+y^2+8x+2y+8=0交于A,B两点, 2020-04-26 …
已知椭圆T的方程为x^2/a^2+y^2/b^2=1(a>b>0),A(0,b),B(0,-b)和 2020-04-27 …
补全对话A:hi,Kate.youlooksoworried.what'sthematter?B: 2020-05-13 …
数量积问题,若a平行于b,且存在不等于零的实数k,t使得[a(t^2-3)b]向量a=(√3,-1 2020-05-14 …
利用立方和,立方差公式,完全立方公式分解因式,数学高手帮帮忙=(利用立方和,立方差公式,完全立方公 2020-05-14 …
matlab 结果用参数表示syms t a b c h;u=a/(4*3*2*1)*t^4+b/ 2020-05-16 …
如图,已知点A,B是椭圆x^2/a^2+y^2/b^2=1(a>b>0)的两个顶点,若点C(t,t 2020-06-21 …
设A是n阶矩阵,A=E+xy^T,x与y都是n*1矩阵,且x^T*y=2,求A的特征值、特征向量易 2020-06-30 …
lingo求救急MODEL:SETS:ID/1..4/;NO(ID):a,b,n;endsetsma 2020-12-19 …
已知Ax=0的通解,如何求矩阵A例如A是2*4的矩阵,其基础解系为a1=(1,3,0,2)^T,a2 2021-02-11 …