早教吧作业答案频道 -->数学-->
如图,△ABC中,AB=AC,AD⊥AC,且AD=AC,AF⊥BC,交BD于点F,(1)求证:CF⊥BD;(2)作AG⊥BD于G,求证:DF-CF=2AG.
题目详情
如图,△ABC中,AB=AC,AD⊥AC,且AD=AC,AF⊥BC,交BD于点F,
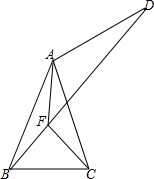
(1)求证:CF⊥BD;
(2)作AG⊥BD于G,求证:DF-CF=2AG.

(1)求证:CF⊥BD;
(2)作AG⊥BD于G,求证:DF-CF=2AG.
▼优质解答
答案和解析
(1)证明:设AC与BD交于点O.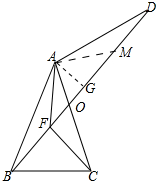
∵AB=AC,AF⊥BC,
∴AF垂直平分BC,
∴FB=FC,
∴∠ABC=∠ACB,∠FBC=∠FCB,
∴∠ABF=∠ACF,
∵AB=AD,
∴∠ABF=∠ADB=∠ACF,
∵∠AOD=∠FOC,∠DAO+∠AOD+∠D=180°,∠OFC+∠FOC+∠OCF=180°,
∴∠OFC=∠DAO=90°,
∴CF⊥BD.
(2)在DB上截取AM=AF.
∵FB=FC,∠BFC=90°,
∴∠FBC=∠FCB=45°,
∴2∠FAC+2∠FCA=90°,
∴∠FAC+∠FCA=45°,
∵AG⊥BD,CF⊥BD,
∴AG∥CF,
∴∠FCA=∠OAG,
∴∠FAG=∠FAC+∠OAG=∠FAO+∠ACF=45°,
∴∠AFM=∠AMF=∠FAG=∠GAM=45°,
∴∠AMD=∠AFC=135°,AG=FG=GM,
在△ACF和△ADM中,
,
∴△ACF≌△ADM,
∴DM=CF,
∴DF-CF=DM+2AG-CF=2AG.

∵AB=AC,AF⊥BC,
∴AF垂直平分BC,
∴FB=FC,
∴∠ABC=∠ACB,∠FBC=∠FCB,
∴∠ABF=∠ACF,
∵AB=AD,
∴∠ABF=∠ADB=∠ACF,
∵∠AOD=∠FOC,∠DAO+∠AOD+∠D=180°,∠OFC+∠FOC+∠OCF=180°,
∴∠OFC=∠DAO=90°,
∴CF⊥BD.
(2)在DB上截取AM=AF.
∵FB=FC,∠BFC=90°,
∴∠FBC=∠FCB=45°,
∴2∠FAC+2∠FCA=90°,
∴∠FAC+∠FCA=45°,
∵AG⊥BD,CF⊥BD,
∴AG∥CF,
∴∠FCA=∠OAG,
∴∠FAG=∠FAC+∠OAG=∠FAO+∠ACF=45°,
∴∠AFM=∠AMF=∠FAG=∠GAM=45°,
∴∠AMD=∠AFC=135°,AG=FG=GM,
在△ACF和△ADM中,
|
∴△ACF≌△ADM,
∴DM=CF,
∴DF-CF=DM+2AG-CF=2AG.
看了 如图,△ABC中,AB=AC...的网友还看了以下:
写出下列自然大调的音阶:G,D,F,降B,降E,A,E,B,降A,降D.好的奖50,快,有赏:写出 2020-05-16 …
悬挂一物体P,绳的拉力为F,物体的重力为G,则下列说法正确的是()A,F与G大小相等,且方向相反. 2020-05-21 …
谁能证明一下这个有关除法的商和余数的规律?设:a/b=c.da/10b=e.f则:f/b=g.h1 2020-05-22 …
若某二叉树采用广义表(A(B(E),C(F(H,G),D)))表示,该二叉树的中序遍历序列为(47) 2020-05-26 …
一道高数函数连续性的问题!谢谢!设f(x)在x0连续,g(x)在x0不连续,则在x0处()A.f( 2020-06-06 …
单选,但是我不知道如何解出来,以及其他选项错在哪里设x→x0时,f(x)与g(x)均为(x-x0) 2020-06-14 …
设f(x),g(x)在[a,b]上连续,且均为严格单增的正函数,证明:存在c€(a,b)使f(b) 2020-06-18 …
f(x),g(x),h(x)在[a,b]上连续,(a,b)上可导,求证存在一个e属于(a,b)使得 2020-07-16 …
多选若果∫df(x)=∫dg(x),则必有A.f'(x)=g'(x)B.df(x)=dg(x)C.f 2020-11-02 …
多选若果∫df(x)=∫dg(x),则必有A.f'(x)=g'(x)B.df(x)=dg(x)C.f 2020-11-02 …