早教吧作业答案频道 -->数学-->
已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD.(1)若∠COD=180°-α时,探索下面两个问题:①如图1,当OC在OD左侧,求∠MON的度数;②当OC在OD右侧,请在图2内
题目详情
已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD.
(1)若∠COD=180°-α时,探索下面两个问题:
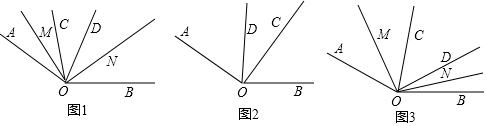
①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)如图3,当∠COD=kα,且OC在OD左侧时,直接写出∠MON的度数(用含α、k的代数式表示).
(1)若∠COD=180°-α时,探索下面两个问题:
①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)如图3,当∠COD=kα,且OC在OD左侧时,直接写出∠MON的度数(用含α、k的代数式表示).

▼优质解答
答案和解析
 (1)①如图1,∵OM平分∠AOC,ON平分∠BOD,
(1)①如图1,∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=
∠AOC,∠BON=
∠BOD,
∴∠AOM+∠BON=
(∠AOC+∠BOD),
∵∠AOB=α,∠COD=180°-α,
∴∠AOC+∠BOD=∠AOB-∠COD=α-(180°-α)=2α-180°,
∴∠AOM+∠BON=
(2α-180°)=α-90°,
∴∠MON=∠AOB-(∠AOM+∠BON)=α-(α-90°)=90°;
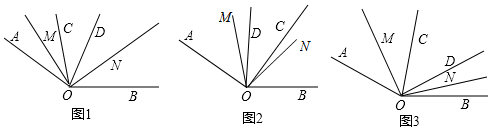
②当OC在OD右侧,补全图形如图2所画,
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=
∠AOC,∠BON=
∠BOD,
∵∠AOB=α,∠COD=180°-α,
∴∠AOC+∠BOD=∠AOB+∠COD=α+(180°-α)=180°,
∴∠AOM+∠BON=
×180°=90°,
∴∠MON=∠AOB-(∠AOM+∠BON)=α-90°;
(2)∠MON的度数为
(1+k)α.
理由:如图3,∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=
∠AOC,∠BON=
∠BOD,
∴∠AOM+∠BON=
(∠AOC+∠BOD),
∵∠AOB=α,∠COD=kα,
∴∠AOC+∠BOD=∠AOB-∠COD=α-kα,
∴∠AOM+∠BON=
(α-kα)=
α(1-k),
∴∠MON=∠AOB-(∠AOM+∠BON)=α-
α(1-k)=
(1+k)α.
 (1)①如图1,∵OM平分∠AOC,ON平分∠BOD,
(1)①如图1,∵OM平分∠AOC,ON平分∠BOD,∴∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOM+∠BON=
| 1 |
| 2 |
∵∠AOB=α,∠COD=180°-α,
∴∠AOC+∠BOD=∠AOB-∠COD=α-(180°-α)=2α-180°,
∴∠AOM+∠BON=
| 1 |
| 2 |
∴∠MON=∠AOB-(∠AOM+∠BON)=α-(α-90°)=90°;
②当OC在OD右侧,补全图形如图2所画,
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=α,∠COD=180°-α,
∴∠AOC+∠BOD=∠AOB+∠COD=α+(180°-α)=180°,
∴∠AOM+∠BON=
| 1 |
| 2 |
∴∠MON=∠AOB-(∠AOM+∠BON)=α-90°;
(2)∠MON的度数为
| 1 |
| 2 |
理由:如图3,∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOM+∠BON=
| 1 |
| 2 |
∵∠AOB=α,∠COD=kα,
∴∠AOC+∠BOD=∠AOB-∠COD=α-kα,
∴∠AOM+∠BON=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠AOB-(∠AOM+∠BON)=α-
| 1 |
| 2 |
| 1 |
| 2 |
看了 已知∠AOB=α(90°<α...的网友还看了以下:
a个人n天完成一项工作,那么平均每人每天的工作量为 用字母表示 2020-04-05 …
a个人n天完成一项工作,平均每人每天工作量为( ) 2020-04-05 …
a个人n天完成一项工作,平均每人每天工作量为( )为什么 (an)分之1 ) 2020-04-05 …
已知全集U=N,集合A={x | x=2n,n∈N} ,B={x | x=4n,n∈N},则A . 2020-04-06 …
#includemain(){inta=0x7fffffff,b=025;floatf1=123. 2020-05-19 …
哪位好心人帮我回答两道一元一次方程题1.若a,c,d是整数,b是正整数,且满足a+b=c,b+c= 2020-05-21 …
帮忙解决两个抽屉原理的问题18个班,每个班有40个人,若10人同班,至少抽多少人?M种颜色小球,每 2020-06-05 …
求教数学题一道如果n是一个大于6的整数,那下面哪一个一定能被3整除?A.N*(N+5)(N-6)B 2020-06-12 …
求证:1\a(a+d)+1\(a+d)(a+2d)+.+1\[a+(n-2)d][a+(n-1)d 2020-06-12 …
编程,从键盘输入1个人的工资(1000—9999之间的整数),计算给这个人发工资时,需面值100元 2020-07-18 …