早教吧作业答案频道 -->物理-->
如图,轨道CDGH位于竖直平面内,其中圆弧段DG与水平段CD及倾斜段GH分别相切于D点和G点,圆弧段和倾斜段均光滑,在H处固定一垂直于轨道的绝缘挡板,整个轨道绝缘且处于水平向右的匀强电
题目详情
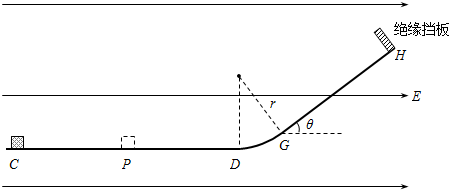
如图,轨道CDGH位于竖直平面内,其中圆弧段DG与水平段CD及倾斜段GH分别相切于D点和G点,圆弧段和倾斜段均光滑,在H处固定一垂直于轨道的绝缘挡板,整个轨道绝缘且处于水平向右的匀强电场中.一带电物块由C处静止释放,经挡板碰撞后滑回CD段中点P处时速度恰好为零.已知物块的质量m=4×10-3kg,所带的电荷量q=+3×10-6C;电场强度E=1×104N/C;CD段的长度L=0.8m,圆弧DG的半径r=0.2m,GH段与水平面的夹角为θ,且sinθ=0.6,cosθ=0.8;不计物块与挡板碰撞时的动能损失,物块可视为质点,重力加速度g取10m/s2.
(1)求物块与轨道CD段的动摩擦因数µ;
(2)求物块第一次碰撞挡板时的动能Ek;
(3)分析说明物块在轨道CD段运动的总路程能否达到2.6m.若能,求物块在轨道CD段运动2.6m路程时的动能;若不能,求物块碰撞挡板时的最小动能.

(1)求物块与轨道CD段的动摩擦因数µ;
(2)求物块第一次碰撞挡板时的动能Ek;
(3)分析说明物块在轨道CD段运动的总路程能否达到2.6m.若能,求物块在轨道CD段运动2.6m路程时的动能;若不能,求物块碰撞挡板时的最小动能.
▼优质解答
答案和解析
(1)物块由C处释放后经挡板碰撞滑回P点过程中,由动能定理得
qE
-μmg(L+
)=0
解得μ=
=0.25;
(2)物块在GH段运动时,由于qEcosθ=mgsinθ,所以做匀速直线运动
由C运动至H过程中,由动能定理得
qEL-μmgL+qErsinθ-mgr(1-cosθ)=Ek-0
解得Ek=0.018J;
(3)物块最终会在DGH间来回往复运动,物块在D点的速度为0
设物块能在水平轨道上运动的总路程为s,由能量守恒定律可得
qEL=μmgs
解得s=2.4m
因为2.6m>s,所以不能在水平轨道上运动2.6m的路程
物块碰撞挡板的最小动能E0等于往复运动时经过G点的动能,由动能定理得
qErsinθ-mgr(1-cosθ)=E0-0
解得E0=0.002J.
答:(1)物块与轨道CD段的动摩擦因数µ为0.25;
(2)物块第一次碰撞挡板时的动能Ek为0.018J;
(3)物块在轨道CD段运动的总路程不能达到2.6m,物块碰撞挡板时的最小动能为0.002J.
qE
| L |
| 2 |
| L |
| 2 |
解得μ=
| qE |
| 3mg |
(2)物块在GH段运动时,由于qEcosθ=mgsinθ,所以做匀速直线运动
由C运动至H过程中,由动能定理得
qEL-μmgL+qErsinθ-mgr(1-cosθ)=Ek-0
解得Ek=0.018J;
(3)物块最终会在DGH间来回往复运动,物块在D点的速度为0
设物块能在水平轨道上运动的总路程为s,由能量守恒定律可得
qEL=μmgs
解得s=2.4m
因为2.6m>s,所以不能在水平轨道上运动2.6m的路程
物块碰撞挡板的最小动能E0等于往复运动时经过G点的动能,由动能定理得
qErsinθ-mgr(1-cosθ)=E0-0
解得E0=0.002J.
答:(1)物块与轨道CD段的动摩擦因数µ为0.25;
(2)物块第一次碰撞挡板时的动能Ek为0.018J;
(3)物块在轨道CD段运动的总路程不能达到2.6m,物块碰撞挡板时的最小动能为0.002J.
看了 如图,轨道CDGH位于竖直平...的网友还看了以下:
高中同步卫星人造卫星先在I轨道上运动,然后改在轨道II上运动,最后在轨道III上运动.在轨道I上速度 2020-03-30 …
竖直平面内有固定轨道ABCO,AB段水平,长为4m;BCO段弯曲且光滑,轨道在0点的曲率半径为1. 2020-04-05 …
一篇心愿作文500字,小范围的如在下个学期进步让我的xxx赶快恢复等. 2020-05-13 …
如图所示,一对平行光滑轨道放置在水平面上,两轨道间距,电阻R=1Ω;有一导体杆静止地放在轨道上,与 2020-05-14 …
EXCEL带单位计算的方法现有答案好像没有适合我的.如在A1内输入:(2.21米+3.8米)*0. 2020-05-17 …
如图所示,在匀强磁场中竖直放置两条足够长的平行轨道,磁场方向与导轨所在平面垂直.磁感应强度大小为B 2020-05-17 …
如图所示,倾角为θ=45°的直导轨与半径为R的圆环轨道相切,切点为B,整个轨道处在竖直平面内,一质 2020-05-17 …
航天员脱离飞船飞向太空会是什么结果?如果在轨道会怎么样,如果不再轨道会怎么样?会在太空存活多长时间 2020-05-20 …
电荷流动方向与导体问,当电荷在什么导体中分别是怎样流动的如在金属导体中,为负电荷运动.那别的一些情 2020-05-22 …
质量为0.5kg的金属杆在相距1m的水平轨道上与轨道垂直放置,如图所示,匀强磁场B垂直轨道平面,金 2020-05-23 …