对任意的正数x，都存在两个不同的正数y，使x2（lny-lnx）-ay2=0成立，则实数a的取值范围为（）A.（0，12e）B.（-∞，12e）C.（12e，+∞）D.（12e，1）

Question

对任意的正数x，都存在两个不同的正数y，使x²（lny-lnx）-ay²=0成立，则实数a的取值范围为（　　）

A. （0，

(1)/(2e)）

B. （-∞，

(1)/(2e)）

C. （

(1)/(2e)，+∞）

D. （

(1)/(2e)，1）

Answer 1

由x²（lny-lnx）-ay²=0（x，y>0），可得：a=(ln(y)/(x))/(((y)/(x))2)，令(y)/(x)=t>0，∴a=(lnt)/(t2)，
设g（t）═(lnt)/(t2)，g′（t）=((1)/(t)×t2-2tlnt)/(t4)=(1-2lnt)/(t3)．
令g′（t）>0．解得0<t<√(e)，此时函数g（t）单调递增；
令g′（t）<0．解得t>√(e)，此时函数g（t）单调递减．
又t>1时，g（t）>0；1>t>0时，g（t）<0．
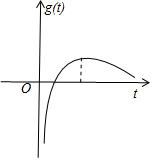
可得函数g（t）的图象．
因此当a∈(0，(1)/(2e))时，存在两个正数，使得a=(lnt)/(t2)成立，
即对任意的正数x，都存在两个不同的正数y，
使x²（lny-lnx）-ay²=0成立．
故选：A．