早教吧作业答案频道 -->数学-->
已知抛物线的表达式为y=-x2+6x+c.(1)若抛物线与x轴有交点,求c的取值范围;(2)设抛物线与x轴两个交点的横坐标分别为x1、x2,若x12+x22=26,求c的值;(3)若P、Q是抛物线上位于第一象限
题目详情
已知抛物线的表达式为y=-x2+6x+c.
(1)若抛物线与x轴有交点,求c的取值范围;
(2)设抛物线与x轴两个交点的横坐标分别为x1、x2,若x12+x22=26,求c的值;
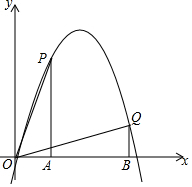
(3)若P、Q是抛物线上位于第一象限的不同两点,PA、QB都垂直于x轴,垂足分别为A、B,且△OPA与△OQB全等,求证:c>-
.

(1)若抛物线与x轴有交点,求c的取值范围;
(2)设抛物线与x轴两个交点的横坐标分别为x1、x2,若x12+x22=26,求c的值;
(3)若P、Q是抛物线上位于第一象限的不同两点,PA、QB都垂直于x轴,垂足分别为A、B,且△OPA与△OQB全等,求证:c>-
| 21 |
| 4 |
▼优质解答
答案和解析
(1)∵抛物线与x轴有交点,
∴b2-4ac≥0,
∴36+4c≥0,
∴x≥-9.
(2)∵x1+x2=6,x1x2=-c,
∴x12+x22=(x1+x2)2-2x1x2=36+2c=26
∴c=-5.
(3)∵△OPA≌△QOB,
∴OA=BQ,AP=OB,
∴可以设P(m,n),则Q(n,m)
将P(m,n),Q(n,m)代入原解析式中得:
①-②得:n2-m2+6m-6n=n-m
∴n2-m2+7m-7n=0,
∴(n-m)(n+m-7)=0,
∴m=n或m=7-n,
∵m,n不相等,
∴m=7-n,
将m=7-n代入①得:n2-7n+7-c=0,
∵b2-4ac>0,
∴49-4(7-c)>0,
∴c>-
.
∴b2-4ac≥0,
∴36+4c≥0,
∴x≥-9.
(2)∵x1+x2=6,x1x2=-c,
∴x12+x22=(x1+x2)2-2x1x2=36+2c=26
∴c=-5.

(3)∵△OPA≌△QOB,
∴OA=BQ,AP=OB,
∴可以设P(m,n),则Q(n,m)
将P(m,n),Q(n,m)代入原解析式中得:
|
①-②得:n2-m2+6m-6n=n-m
∴n2-m2+7m-7n=0,
∴(n-m)(n+m-7)=0,
∴m=n或m=7-n,
∵m,n不相等,
∴m=7-n,
将m=7-n代入①得:n2-7n+7-c=0,
∵b2-4ac>0,
∴49-4(7-c)>0,
∴c>-
| 21 |
| 4 |
看了 已知抛物线的表达式为y=-x...的网友还看了以下:
电荷量不等的两点电荷固定在x轴上坐标为-3L和3L的两点,其中坐标为3L处电荷带正电,电荷量为Q. 2020-05-13 …
在平面直角坐标系xOy的第一象限内充满匀强磁场,磁场方向垂直于纸面向外,磁感应强度的大小为B.在y 2020-05-14 …
在如图所示的空间坐标系中,y轴的左边有一匀强电场,场强大小为E,场强方向跟y轴负向成30°,y的右 2020-05-17 …
如图所示,在x轴上坐标为+1m的点上固定一个电量为+4Q的点电荷,坐标原点O处固定一电量为一Q的点 2020-06-14 …
如图,在平面直角坐标系xoy中,点A在y轴上坐标为(0,3),点B在x轴上坐标为(10,0),BC 2020-06-14 …
如图所示,在x轴上坐标为1的点上固定一个电荷量为4Q的正点电荷,坐标原点O处固定一个电荷量为-Q的 2020-06-14 …
以0为中心,焦点在实轴上,长轴为a,短半轴为b的椭圆周用复参数方程表示 2020-07-30 …
如图,已知A〔4.0〕动点P〔0.a〕〔1〕:若PA小于5,你能写出a所满足的不等式吗?2:若PA 2020-08-03 …
如图所示,在第一象限有向下的匀强电场,在第四象限有垂直纸面向里的有界匀强磁场.在y轴上坐标为(0,b 2020-10-30 …
如图7,在平面直角坐标系中,已知A(0,2),C(1,0),AB⊥AC,求点B的坐标图是一个坐标A在 2020-11-03 …