早教吧作业答案频道 -->数学-->
设m∈R,在平面直角坐标系中,已知向量,向量,,动点M(x,y)的轨迹为E.(Ⅰ)求轨迹E的方程,并说明该方程所表示曲线的形状;(Ⅱ)已知m=,证明:存在圆心在原点的圆
题目详情
设m∈R,在平面直角坐标系中,已知向量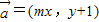 ,向量
,向量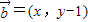 ,
,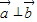 ,动点M(x,y)的轨迹为E.
,动点M(x,y)的轨迹为E.
(Ⅰ)求轨迹E的方程,并说明该方程所表示曲线的形状;
(Ⅱ)已知m= ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程.
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程.
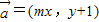 ,向量
,向量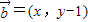 ,
,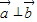 ,动点M(x,y)的轨迹为E.
,动点M(x,y)的轨迹为E.(Ⅰ)求轨迹E的方程,并说明该方程所表示曲线的形状;
(Ⅱ)已知m=
 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程.
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程.▼优质解答
答案和解析
分析:
(1)因为,,,所以,由此根据实数m的取值,能判断该方程所表示曲线的形状.(2)当m=时,轨迹E的方程为,设圆心在原点的圆的一条切线为y=kx+t,解方程组,得x2+4(kx+t)2=4,即(1+4k2)x2+8ktx+4t2-4=0,由此证明存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程.
(1)因为,,,所以,即mx2+y2=1.当m=0时,方程表示两直线,方程为y=±1;当m=1时,方程表示圆;当m>0且m≠1时,方程表示的是椭圆;当m<0时,方程表示的是双曲线.(2)当m=时,轨迹E的方程为,设圆心在原点的圆的一条切线为y=kx+t,解方程组,得x2+4(kx+t)2=4,即(1+4k2)x2+8ktx+4t2-4=0,要使切线与轨迹E恒有两个交点A,B,则使△=64k2t2-16(1+4k2)(t2-1)=16(4k2-t2+1)>0,即4k2-t2+1>0,即t2<4k2+1,且y1y2=(kx1+t)(kx2+t)==+t2=,要使,需使x1x2+y1y2=0,即=,所以5t2-4k2-4=0,即5t2=4k2+4且t2<4k2+1,即4k2+4<20k2+5恒成立.所以又因为直线y=kx+t为圆心在原点的圆的一条切线,所以圆的半径为,=,所求的圆为.当切线的斜率不存在时,切线为,与交于点或也满足OA⊥OB.综上,存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且.
点评:
本题考查方程所表示曲线形状,考查圆的方程的求法.解题时要认真审题,仔细解答,注意直线和圆锥曲线的位置关系的综合应用.
分析:
(1)因为,,,所以,由此根据实数m的取值,能判断该方程所表示曲线的形状.(2)当m=时,轨迹E的方程为,设圆心在原点的圆的一条切线为y=kx+t,解方程组,得x2+4(kx+t)2=4,即(1+4k2)x2+8ktx+4t2-4=0,由此证明存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程.
(1)因为,,,所以,即mx2+y2=1.当m=0时,方程表示两直线,方程为y=±1;当m=1时,方程表示圆;当m>0且m≠1时,方程表示的是椭圆;当m<0时,方程表示的是双曲线.(2)当m=时,轨迹E的方程为,设圆心在原点的圆的一条切线为y=kx+t,解方程组,得x2+4(kx+t)2=4,即(1+4k2)x2+8ktx+4t2-4=0,要使切线与轨迹E恒有两个交点A,B,则使△=64k2t2-16(1+4k2)(t2-1)=16(4k2-t2+1)>0,即4k2-t2+1>0,即t2<4k2+1,且y1y2=(kx1+t)(kx2+t)==+t2=,要使,需使x1x2+y1y2=0,即=,所以5t2-4k2-4=0,即5t2=4k2+4且t2<4k2+1,即4k2+4<20k2+5恒成立.所以又因为直线y=kx+t为圆心在原点的圆的一条切线,所以圆的半径为,=,所求的圆为.当切线的斜率不存在时,切线为,与交于点或也满足OA⊥OB.综上,存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且.
点评:
本题考查方程所表示曲线形状,考查圆的方程的求法.解题时要认真审题,仔细解答,注意直线和圆锥曲线的位置关系的综合应用.
看了 设m∈R,在平面直角坐标系中...的网友还看了以下:
在溶液配制过程中,下列操作使配制结果偏高的是哪些?A.将药品放入容量瓶中加蒸馏水溶解B.容量瓶在使 2020-04-12 …
配制100mL1.0mol•L-1的NaOH溶液,下列情况会导致溶液浓度偏高的是()A.容量瓶使用 2020-04-12 …
关于位移与路程,下列说法正确的是()A.位移与路程都是矢量B.位移是矢量,路程是标量C.路程一定等 2020-05-14 …
关于位移与路程,下列说法正确的是()A.位移与路程都是矢量B.位移是矢量,路程是标量C.路程一定等 2020-05-14 …
知道地面高程,设计高程和标高如何算填挖量桩号 设计高程 地面高程 测得标高 填土量 挖土量k24+ 2020-05-17 …
看线段图写数量关系式,再列出方程.数量关系式总重量×5九=20总重量×5九=20&nbs图;&nb 2020-07-18 …
把装有适量水的量筒倒置在水槽里的水中,量筒口未接触水槽底部,量筒中的水面高于水槽中的水面,且水面是静 2020-12-15 …
关于一列简谐波,下面说法中正确的是()A.波动的产生需要两个条件,即波源和传播波介质B.波动过程是质 2020-12-18 …
下面有关能量转化和守恒的说法中正确的是()A.我们在使用能量的过程,就是能量的转化和转移的过程B.能 2020-12-22 …
电压表(1)用途:测量电路两端电压的大小,其符号是.(2)使用方法a.认清量程:双量程,分别是0~3 2020-12-31 …