早教吧作业答案频道 -->数学-->
在平面直角坐际系xOy中,P是椭圆y24+x23=1上的一个动点,点A(1,1),B(0,-1),则|PA|+|PB|的最大值为()A.2B.3C.4D.5
题目详情
在平面直角坐际系xOy中,P是椭圆
+y2 4
=1上的一个动点,点A(1,1),B(0,-1),则|PA|+|PB|的最大值为( )x2 3
A. 2
B. 3
C. 4
D. 5
▼优质解答
答案和解析
 ∵椭圆方程为
∵椭圆方程为
+
=1,
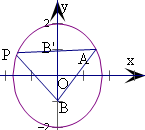
∴焦点坐标为B(0,-1)和B'(0,1),
连接PB'、AB',根据椭圆的定义,
得|PB|+|PB'|=2a=4,可得|PB|=4-|PB'|,
因此|PA|+|PB|=|PA|+(4-|PB'|)=4+(|PA|-|PB'|)
∵|PA|-|PB'|≤|AB'|
∴|PA|+|PB|≤2a+|AB'|=4+1=5.
当且仅当点P在AB'延长线上时,等号成立.
综上所述,可得|PA|+|PB|的最大值为5.
故选:D.
 ∵椭圆方程为
∵椭圆方程为| y2 |
| 4 |
| x2 |
| 3 |
∴焦点坐标为B(0,-1)和B'(0,1),
连接PB'、AB',根据椭圆的定义,
得|PB|+|PB'|=2a=4,可得|PB|=4-|PB'|,
因此|PA|+|PB|=|PA|+(4-|PB'|)=4+(|PA|-|PB'|)
∵|PA|-|PB'|≤|AB'|
∴|PA|+|PB|≤2a+|AB'|=4+1=5.
当且仅当点P在AB'延长线上时,等号成立.
综上所述,可得|PA|+|PB|的最大值为5.
故选:D.
看了 在平面直角坐际系xOy中,P...的网友还看了以下:
对于正比例函数y=2x,下列判断正确的是()A.自变量x的值毎增加1,函数y的值增加2B.自变量x的 2020-03-30 …
求解一道西方经济学题目货币需求函数是m=0.8y-8兆×r.这里,y是实际GDP,r是利率,单位为 2020-04-27 …
一、已知y=2-3x分之x-1,x取那些值时(1)y的值是正数(2)y的值是负数(3)y的值是零( 2020-05-14 …
英语翻译我支付了XXCNY的关税海关按照你们的申报价值征税,并没有查询实际价值如果按照实际价格征税 2020-05-16 …
已知方程组2x+y=5m+6,x-2y=-17的解x、y都是正数,且x的值小于y的值,求x的取值范 2020-05-16 …
面积是30的梯形,其上底是下底长的1/3,已知上底长为x,高为y.y与x的函数表达式为(),y是x 2020-05-24 …
二次函数和实际问题在二次函数的实际应用里如果一个实际问题算出了他的解析式,并求出了他的取值范围,但 2020-06-06 …
1.已知:点P(x,y)在X轴的下方,且x,y是方程组{2x+3y=2k-1的解,求K的取值范围. 2020-06-30 …
弹簧秤的弹簧在中点处被折断后,把两段弹簧并联起来装进弹簧秤,校正零点后用它去测力,结果是()A.测 2020-06-30 …
牧场中羊群的最大养殖量为m,为了保证羊群的生长空间,实际养殖量x小于m,以便留出适当的空闲量m-x 2020-07-11 …