早教吧作业答案频道 -->数学-->
如图,已知抛物线C1:y=14x2,圆C2:x2+(y-1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.(1)求点A,B的坐标;(2)求△PAB的面积.
题目详情
如图,已知抛物线C1:y=
x2,圆C2:x2+(y-1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.
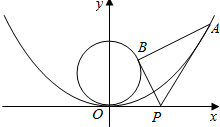
(1)求点A,B的坐标;
(2)求△PAB的面积.
| 1 |
| 4 |

(1)求点A,B的坐标;
(2)求△PAB的面积.
▼优质解答
答案和解析
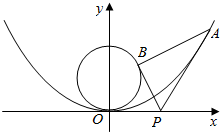 (1)由直线PA的斜率存在,设切线PA的方程为:y=k(x-t)(k≠0),联立抛物线,化为x2-4kx+4kt=0,
(1)由直线PA的斜率存在,设切线PA的方程为:y=k(x-t)(k≠0),联立抛物线,化为x2-4kx+4kt=0,
∵△=16k2-16kt=0,解得k=t,
∴x=2t,∴A(2t,t2).
圆C2的圆心D(0,1),设B(x0,y0),由题意可知:点B与O关于直线PD得出
,
∴解得x0=
,y0=
.
∴B(
,
).
(2)由(1)可得:kAB=
,直线AB的方程为:y-t2=
(x-2t),化为(t2-1)x-2ty+2t=0,
∴点P到直线AB的距离d=
=t,
又|AB|=
=t2.
∴S△PAB=
t3.
 (1)由直线PA的斜率存在,设切线PA的方程为:y=k(x-t)(k≠0),联立抛物线,化为x2-4kx+4kt=0,
(1)由直线PA的斜率存在,设切线PA的方程为:y=k(x-t)(k≠0),联立抛物线,化为x2-4kx+4kt=0,∵△=16k2-16kt=0,解得k=t,
∴x=2t,∴A(2t,t2).
圆C2的圆心D(0,1),设B(x0,y0),由题意可知:点B与O关于直线PD得出
|
∴解得x0=
| 2t |
| 1+t2 |
| 2t2 |
| 1+t2 |
∴B(
| 2t |
| 1+t2 |
| 2t2 |
| 1+t2 |
(2)由(1)可得:kAB=
| t2-1 |
| 2t |
| t2-1 |
| 2t |
∴点P到直线AB的距离d=
| |(t2-1)t+2t| | ||
|
又|AB|=
(
|
∴S△PAB=
| 1 |
| 2 |
看了 如图,已知抛物线C1:y=1...的网友还看了以下:
微积分求弧长公式以知2点(0,h)(d,h)弧长=L/B*D顶点=(d/2,主Y)只有Y是未知的其 2020-04-26 …
请问已知2点坐标a(5,8);b(13,21)怎么用三角函数式表达ab二点间的斜率?按照直线斜率公 2020-05-13 …
已知2点坐标求一元一次方程已知两点坐标A(a,b),B(c,d),求此直线的一元一次方程.注:a, 2020-06-13 …
已知2点坐标和半径怎么求圆心坐标?比如点A坐标x=0,y=15,B点坐标x=40,y=0.半径16 2020-06-14 …
关于一个解析几何方程.(坐标系转换)请问一个问题.坐标系转换.已经A,B两点的旧坐标系坐标和新坐标 2020-08-02 …
已知2点坐标[x1y1][x2y2]怎样求解析式啊?讲得明白点我听说有个公式可以往里套是什么啊?不好 2020-11-29 …
求个数学公式已知2点坐标xy求2点中间点的坐标xy还有个问题如果不求中间点而是要求距离第一个点已知距 2020-12-03 …
请问全站仪放样详细步骤,请别复制说明书.已知1点x=10000.000y=-10000.000已知2 2020-12-30 …
工程测量中放样,已知2点坐标,怎么样放样出2点延长线上的任意一点? 2020-12-30 …
谁能给我详细解答一下红磷燃烧的实验谁能给我详细解答一下红磷在氧气中燃烧产生五氧化二磷的化学实验?包括 2021-02-02 …