早教吧作业答案频道 -->数学-->
如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,O是△ABD的外接圆.(1)求证:AC是O的切线;(2)当BD是O的直径时(如图2),求∠CAD的度数.
题目详情
如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3, O是△ABD的外接圆.
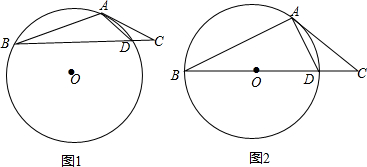
(1)求证:AC是 O的切线;
(2)当BD是 O的直径时(如图2),求∠CAD的度数.

(1)求证:AC是 O的切线;
(2)当BD是 O的直径时(如图2),求∠CAD的度数.
▼优质解答
答案和解析
(1)证明: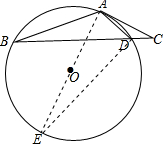 连接AO,延长AO交 O于点E,则AE为 O的直径,连接DE,如图所示:
连接AO,延长AO交 O于点E,则AE为 O的直径,连接DE,如图所示:
∵∠ABC:∠ACB:∠ADB=1:2:3,∠ADB=∠ACB+∠CAD,
∴∠ABC=∠CAD,
∵AE为 O的直径,
∴∠ADE=90°,
∴∠EAD=90°-∠AED,
∵∠AED=∠ABD,
∴∠AED=∠ABC=∠CAD,
∴∠EAD=90°-∠CAD,
即∠EAD+∠CAD=90°,
∴EA⊥AC,
∴AC是 O的切线;
(2) ∵BD是 O的直径,
∴∠BAD=90°,
∴∠ABC+∠ADB=90°,
∵∠ABC:∠ACB:∠ADB=1:2:3,
∴4∠ABC=90°,
∴∠ABC=22.5°,
由(1)知:∠ABC=∠CAD,
∴∠CAD=22.5°.
 连接AO,延长AO交 O于点E,则AE为 O的直径,连接DE,如图所示:
连接AO,延长AO交 O于点E,则AE为 O的直径,连接DE,如图所示:∵∠ABC:∠ACB:∠ADB=1:2:3,∠ADB=∠ACB+∠CAD,
∴∠ABC=∠CAD,
∵AE为 O的直径,
∴∠ADE=90°,
∴∠EAD=90°-∠AED,
∵∠AED=∠ABD,
∴∠AED=∠ABC=∠CAD,
∴∠EAD=90°-∠CAD,
即∠EAD+∠CAD=90°,
∴EA⊥AC,
∴AC是 O的切线;
(2) ∵BD是 O的直径,
∴∠BAD=90°,
∴∠ABC+∠ADB=90°,
∵∠ABC:∠ACB:∠ADB=1:2:3,
∴4∠ABC=90°,
∴∠ABC=22.5°,
由(1)知:∠ABC=∠CAD,
∴∠CAD=22.5°.
看了 如图1,在△ABC中,点D在...的网友还看了以下:
用气枪射击池中的水,要是命中率提高,应瞄准().A.看到鱼的上边.B.看到鱼的下边.就这样. 2020-04-25 …
如果在数轴上表示a和b两个数的点的位置,那么化简|a-b|+|a+b|的结果是多少?a在0的左边, 2020-04-27 …
如图,△OAB中,顶点A的坐标为(2,-3),则△OAB关于y轴对称的△O′A′B′的顶点A′坐标 2020-05-13 …
在三角形ABC中,a,b,c分别是角A,B,C的对边,B=三分之二pai,b=根号13,a+c=4 2020-05-22 …
在三角形ABC中,已知sinA+sinC=2sinB,且B=60度,若三角形ABC的面积为[根号3 2020-06-03 …
解直角三角形中的a边b边c边分别指的是哪三条 2020-06-06 …
求函数f(t)=(1+sint)/(2+cost)的最值.在三角形ABC中,A,B,C成等差数列, 2020-06-06 …
在△ABC中,已知sinA+sinC=2sinB,且∠B=π6,如果△ABC的面积为12,则∠B的 2020-06-06 …
在△ABC中,已知sinA+sinC=2sinB,且B=30°,若△ABC的面积为二分之一,则B的 2020-06-06 …
1、在数轴上,下列各说法正确的是()A-2在-3的左边B-100在0.01的右边C0在0.0001 2020-07-09 …