早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.(1)求点A,B的坐标;(2)求抛物线C1的表达式及
题目详情
在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.
(1)求点A,B的坐标;
(2)求抛物线C1的表达式及顶点坐标;
(3)若抛物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
(1)求点A,B的坐标;
(2)求抛物线C1的表达式及顶点坐标;
(3)若抛物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
▼优质解答
答案和解析
(1)当y=2时,则2=x-1,
解得:x=3,
∴A(3,2),
∵点A关于直线x=1的对称点为B,
∴B(-1,2).
(2)把(3,2),(-1,2)代入抛物线C1:y=x2+bx+c得:
解得:
∴y=x2-2x-1.
顶点坐标为(1,-2).
(3)如图,当C2过A点,B点时为临界,
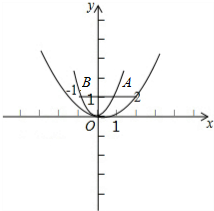
代入A(3,2)则9a=2,
解得:a=
,
代入B(-1,2),则a(-1)2=2,
解得:a=2,
∴
≤a<2.
解得:x=3,
∴A(3,2),
∵点A关于直线x=1的对称点为B,
∴B(-1,2).
(2)把(3,2),(-1,2)代入抛物线C1:y=x2+bx+c得:
|
解得:
|
∴y=x2-2x-1.
顶点坐标为(1,-2).
(3)如图,当C2过A点,B点时为临界,

代入A(3,2)则9a=2,
解得:a=
| 2 |
| 9 |
代入B(-1,2),则a(-1)2=2,
解得:a=2,
∴
| 2 |
| 9 |
看了 在平面直角坐标系xOy中,过...的网友还看了以下:
若f(x)在R上是奇函数,且f(1)=0.f(x)/x的导数大于0(x大于0).则f(x)/x在x小 2020-03-31 …
设f(x)=(1+x)的m次方+(1+x)n次方展开式中x系数是10(m,n属于N+)1.求f(x 2020-05-14 …
如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动 2020-06-08 …
关于反比例函数反比例的区别y与x-1成反比例.当x=时y=时求y与x的函数关系y=2/x-1问:1 2020-06-13 …
平面直角坐标系内点P(x,y)的横坐标x与纵坐标y满足:-1≤x≤1,-1≤y≤1(1)若x属于Z 2020-06-14 …
如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B.P为线段AB上一动 2020-07-19 …
直线X+Y=1于圆x^2+y^2-2ay=0(a大于0)没有公共点,则a的取值范围是? 2020-07-31 …
1若fx在x=0处可导f(0)=0limx趋向于0f(x)/x=?2设fx在x=1处可导且lim△x 2020-11-01 …
已知y加2与x减1成正比例,且x等于3时y等于4.(1)求y与X之间的函数关系式.(5)当y等已知y 2020-11-28 …
对于f(x)中f表示对应关系,那么(x)的含义是什么还有下面这句话应如何理解:函数f(x)对于任何实 2021-01-15 …