早教吧作业答案频道 -->数学-->
在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=α2,连接PB,试探究PA、PB、PC满足的等量关系.(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,
题目详情
在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=
,连接PB,试探究PA、PB、PC满足的等量关系.
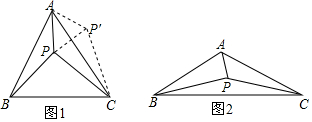
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为___度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为___;
(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
(3)PA、PB、PC满足的等量关系为___.
| α |
| 2 |

(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为___度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为___;
(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
(3)PA、PB、PC满足的等量关系为___.
▼优质解答
答案和解析
(1)∵△ABP≌△ACP′,
∴AP=AP′,
由旋转变换的性质可知,∠PAP′=60°,P′C=PB,
∴△PAP′为等边三角形,
∴∠APP′=60°,
∵∠PAC+∠PCA=
=30°,
∴∠APC=150°,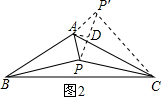
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∴PA2+PC2=PB2,
故答案为:150,PA2+PC2=PB2;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=120°,P′C=PB,
∴∠APP′=30°,
∵∵∠PAC+∠PCA=
=60°,
∴∠APC=120°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=30°,
∴PD=
PA,
∴PP′=
PA,
∴3PA2+PC2=PB2;
(3)如图2,与(2)的方法类似,
作将△ABP绕点A逆时针旋转α得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=α,P′C=PB,
∴∠APP′=90°-
,
∵∵∠PAC+∠PCA=
,
∴∠APC=180°-
,
∴∠P′PC=(180°-
)-(90°-
)=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=90°-
,
∴PD=PA•cos(90°-
)=PA•sin
,
∴PP′=2PA•sin
,
∴4PA2sin2
+PC2=PB2,
故答案为:4PA2sin2
+PC2=PB2.
∴AP=AP′,
由旋转变换的性质可知,∠PAP′=60°,P′C=PB,
∴△PAP′为等边三角形,
∴∠APP′=60°,
∵∠PAC+∠PCA=
| 60° |
| 2 |
∴∠APC=150°,

∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∴PA2+PC2=PB2,
故答案为:150,PA2+PC2=PB2;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=120°,P′C=PB,
∴∠APP′=30°,
∵∵∠PAC+∠PCA=
| 120° |
| 2 |
∴∠APC=120°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=30°,
∴PD=
| ||
| 2 |
∴PP′=
| 3 |
∴3PA2+PC2=PB2;
(3)如图2,与(2)的方法类似,
作将△ABP绕点A逆时针旋转α得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=α,P′C=PB,
∴∠APP′=90°-
| α |
| 2 |
∵∵∠PAC+∠PCA=
| α |
| 2 |
∴∠APC=180°-
| α |
| 2 |
∴∠P′PC=(180°-
| α |
| 2 |
| α |
| 2 |
∴PP′2+PC2=P′C2,
∵∠APP′=90°-
| α |
| 2 |
∴PD=PA•cos(90°-
| α |
| 2 |
| α |
| 2 |
∴PP′=2PA•sin
| α |
| 2 |
∴4PA2sin2
| α |
| 2 |
故答案为:4PA2sin2
| α |
| 2 |
看了 在△ABC中,AB=AC,∠...的网友还看了以下:
关于a/b=40(a,b都是非零自然数),下面说法不正确的是().A.a是b的倍数B.b是40的倍 2020-04-09 …
如果a是有理数,那么下列说法中正确的是A.a一定是正数B.-a一定是负数C.a一定是非负数D.以上 2020-05-13 …
初二题快一点哈已知k=(a+b-c)/c=(a-b+c)/b=(-a+b+c)/a已知k=(a+b 2020-05-13 …
若a是有理数,则下列说法正确的是()A.|a|一定是正数B.|-a|一定是正数C.-|-a|一定是 2020-05-13 …
1、已知a,b,c互不相等求2a-b-c/(a-b)(b-c)+2b-c-a/(b-c)(b-a) 2020-05-16 …
2.空中一只气球只受到竖直方向的一对平衡力作用,则气球 ( C )A.一定静止 B.一定匀速向上运 2020-05-17 …
A,B,C三重量的关系式是A乘B等于C(A,B,C均不等于0)A,B,C三重量的关系式是A乘B等于 2020-06-03 …
甲数的四分之一与乙数的三分之二相等,甲数与乙数()a成正比例,b不成比例在()中,a和b成正比例a 2020-06-03 …
由a=b一定可以得出的等式是()A.a÷c=b÷c由a=b一定可以得出的等式是()A.a÷c=b÷ 2020-06-06 …
a-b+c=a+c-ba+(b-c)=a+b-ca-(b+c)=a-b-ca-(b-c)=a-b+ 2020-06-10 …