早教吧作业答案频道 -->数学-->
在等边△ABC中,D为射线BC上一点,CE是∠ACB外角的平分线,∠ADE=60°,EF⊥BC于F.(1)如图1,若点D在线段BC上.求证:①AD=DE;②BC=DC+2CF;(2)如图2,若点D在线段BC的延长线上,(1)中的两
题目详情
在等边△ABC中,D为射线BC上一点,CE是∠ACB外角的平分线,∠ADE=60°,EF⊥BC于F.
(1)如图1,若点D在线段BC上.求证:①AD=DE;②BC=DC+2CF;
(2)如图2,若点D在线段BC的延长线上,(1)中的两个结论是否仍然成立?请说明理由.
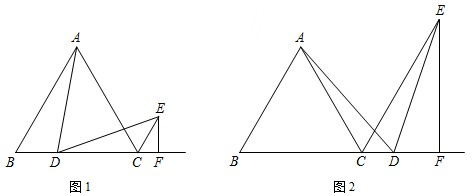
(1)如图1,若点D在线段BC上.求证:①AD=DE;②BC=DC+2CF;
(2)如图2,若点D在线段BC的延长线上,(1)中的两个结论是否仍然成立?请说明理由.

▼优质解答
答案和解析
证明:(1)如图,
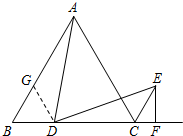
①过D作DG∥AC交AB于G
∵△ABC是等边三角形,AB=BC,
∴∠B=∠ACB=60°
∴∠BDG=∠ACB=60°,
∴∠BGD=60°
∴△BDG是等边三角形,
∴BG=BD
∴AG=DC
∵CE是∠ACB外角的平分线,
∴∠DCE=120°=∠AGD
∵∠ADE=60°,
∴∠ADB+∠EDC=120°=∠ADB+∠DAG
∴∠EDC=∠DAG,
在△AGD和△DCE中,
,
∴△AGD≌△DCE(SAS)
∴AD=DE
②∵△AGD≌△DCE,
∴GD=CE,
∴BD=CE
∴BC=CE+DC=DC+2CF
(2)过D作DG∥AC交AB延长线于G,
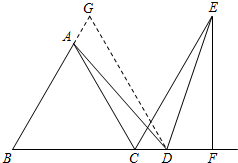
①成立;
∵DG∥AC
AG=DC
∠BFGD=∠BDG=∠B=60°
∠AGD=180°-60°=120°
∵∠ACB=60,CE是∠ACB的外角平分线
∴∠ACE=
×(180°-∠ACB)=60°
∠DCE=120°
∵∠GAD=∠BGD-∠ADG=60°-∠ADG
∵∠CDE=180°-∠GDB-∠ADE-∠ADG=180°-60°-60°-∠ADG=60°-∠ADG
在△AGD和△DCE中,
,
∴△AGD≌△DCE(ASA),
AD=DE
②不成立,此时BC=2CF-CD
∵△AGD≌△DCE,
∴GD=CE,
∴BD=CE
∴BC=BD-CD=CE-DC=2CF-CD.

①过D作DG∥AC交AB于G
∵△ABC是等边三角形,AB=BC,
∴∠B=∠ACB=60°
∴∠BDG=∠ACB=60°,
∴∠BGD=60°
∴△BDG是等边三角形,
∴BG=BD
∴AG=DC
∵CE是∠ACB外角的平分线,
∴∠DCE=120°=∠AGD
∵∠ADE=60°,
∴∠ADB+∠EDC=120°=∠ADB+∠DAG
∴∠EDC=∠DAG,
在△AGD和△DCE中,
|
∴△AGD≌△DCE(SAS)
∴AD=DE
②∵△AGD≌△DCE,
∴GD=CE,
∴BD=CE
∴BC=CE+DC=DC+2CF
(2)过D作DG∥AC交AB延长线于G,

①成立;
∵DG∥AC
AG=DC
∠BFGD=∠BDG=∠B=60°
∠AGD=180°-60°=120°
∵∠ACB=60,CE是∠ACB的外角平分线
∴∠ACE=
| 1 |
| 2 |
∠DCE=120°
∵∠GAD=∠BGD-∠ADG=60°-∠ADG
∵∠CDE=180°-∠GDB-∠ADE-∠ADG=180°-60°-60°-∠ADG=60°-∠ADG
在△AGD和△DCE中,
|
∴△AGD≌△DCE(ASA),
AD=DE
②不成立,此时BC=2CF-CD
∵△AGD≌△DCE,
∴GD=CE,
∴BD=CE
∴BC=BD-CD=CE-DC=2CF-CD.
看了 在等边△ABC中,D为射线B...的网友还看了以下:
已知:反比例函数的图象经过,两点,(1)求反比例函数解析式;(2)若点C(m,1)在此函数图象上, 2020-04-08 …
举例:金属氧化物+非金属氧化物--含氧酸根就是写个化学方程式.符合以上要求的. 2020-05-02 …
请你说一说恰当地运用反义词,对句子表达意思有什么作用?作业上要求的... 2020-05-09 …
HowtoImproveYourEnglish不要有初一没学过的单词,要短,不超过70个单词最符合 2020-05-13 …
为了使经济可持续发展,生产过程应尽量减少对环境的负面作用.由单质铜制取硫酸铜有下列几种步骤,其中可 2020-05-13 …
Σ是平面x-y+z=1在第四卦限部分的上侧,求Σ的面积、、 2020-05-16 …
学校某一天上午,要排数学、语文、外语、体育四节课.数学只能排第一、二节,语文只能排第二、三节,外语 2020-05-16 …
一份公文在结构上要求的是( )。A.完整B.生动C.突出D.简明 2020-05-31 …
往复式压缩机主电机铭牌上标明的功率至少应为压缩机在任何规定的运行条件上要求的最大功率的 2020-05-31 …
英语翻译但是目前看来,很有难度从心理角度来看,这些梦想都是一种向上追求的精神,总是要有梦想,才能继 2020-06-13 …