早教吧作业答案频道 -->数学-->
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.(1)求证:BE=CF;(2)当α=90°时,求四边形AEDC的面积.
题目详情
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.
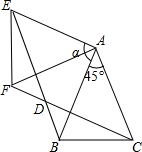
(1)求证:BE=CF;
(2)当α=90°时,求四边形AEDC的面积.

(1)求证:BE=CF;
(2)当α=90°时,求四边形AEDC的面积.
▼优质解答
答案和解析
(1)证明:∵△ABC绕点A按顺时针方向旋转角α得到△AEF,
∴AE=AB,AF=AC,∠EAC=∠BAC,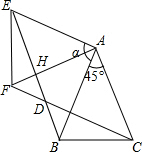
∴AB=AC=AE=AF,∠EAF+∠FAB=∠BAC+∠FAB,即∠EAB=∠FAC,
在△AEB和△AFC中,
,
∴△AEB≌△AFC,
∴BE=CF;
(2) ∵α=90°,即∠EAB=∠FAC=90°,
∵AE=AB,
∴△ABE为等腰直角三角形,
∴∠ABE=45°,
∴∠ABE=∠BAC,
∴AC∥BE,
同理可得AE∥CF,
∵AE=AC,
∴四边形AEDC为菱形,
AF与BE交于点H,如图,
∵∠EAF=45°,
∴AH平分∠EAB,
∴AH⊥BE,
∴△AHE为等腰直角三角形,
∴AH=
AE=
,
∴四边形AEDC的面积=AH•DE=
×2=2
.
∴AE=AB,AF=AC,∠EAC=∠BAC,

∴AB=AC=AE=AF,∠EAF+∠FAB=∠BAC+∠FAB,即∠EAB=∠FAC,
在△AEB和△AFC中,
|
∴△AEB≌△AFC,
∴BE=CF;
(2) ∵α=90°,即∠EAB=∠FAC=90°,
∵AE=AB,
∴△ABE为等腰直角三角形,
∴∠ABE=45°,
∴∠ABE=∠BAC,
∴AC∥BE,
同理可得AE∥CF,
∵AE=AC,
∴四边形AEDC为菱形,
AF与BE交于点H,如图,
∵∠EAF=45°,
∴AH平分∠EAB,
∴AH⊥BE,
∴△AHE为等腰直角三角形,
∴AH=
| ||
| 2 |
| 2 |
∴四边形AEDC的面积=AH•DE=
| 2 |
| 2 |
看了 如图,△ABC中,AB=AC...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
matlab解中学三角函数方程数学题,不会求大大~~~~~~~~~~[a,b,c,A,B,C]=s 2020-05-14 …
1、已知a,b,c互不相等求2a-b-c/(a-b)(b-c)+2b-c-a/(b-c)(b-a) 2020-05-16 …
关于一元二次方程解的情况题:已知实数a,b,c,且a^2+b^2+c^2=a+b+c=2,求a,b 2020-05-17 …
分解因式(a-b-c)(a+b-c)-(b-c-a)(b+c-a)正确答案是这个:(a+b-c)( 2020-05-17 …
在△ABC中,已知sin[B+(C/2)]=4/5,求cos(A-B)的值.过程中有一步不懂,co 2020-06-03 …
初中数学c/(c-b)=-c(a-b)/(b-c)(a-b)c/(c-b)=-c(a-b)/(b- 2020-06-06 …
已知a+b+c=0,试求a^2/(2a^2+bc)+b^2/(2b^2+ac)+c^2/(2c^2 2020-06-11 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
已知a、b、c满足a<b<c,ab+bc+ac=0,abc=1,则()A.|a+b|>|c|B.|a 2020-11-01 …