如图，四边形ABCD是边长为2，一个锐角等于60°的菱形纸片，小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合，按顺时针方向旋转三角形纸片，使它的两边分别

Question

如图，四边形 ABCD 是边长为 2 ，一个锐角等于 60 ° 的菱形纸片，小芳同学将一个三角形纸片的一个顶点与该菱形顶点 D 重合，按顺时针方向旋转三角形纸片，使它的两边分别交 CB 、 BA （或它们的延长线）于点 E 、 F ， ∠ EDF=60 ° ，当 CE=AF 时，如图 1 小芳同学得出的结论是 DE=DF ．

（ 1 ）继续旋转三角形纸片，当 CE ≠ AF 时，如图 2 小芳的结论是否成立？若成立，加以证明；若不成立，请说明理由；

（ 2 ）再次旋转三角形纸片，当点 E 、 F 分别在 CB 、 BA 的延长线上时，如图 3 请直接写出 DE 与 DF 的数量关系；

（ 3 ）连 EF ，若 △ DEF 的面积为 y ， CE=x ，求 y 与 x 的关系式，并指出当 x 为何值时， y 有最小值，最小值是多少？

Answer 1

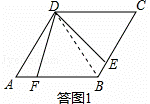
（ 1 ） DF=DE ．理由如下：

如答图 1 ，连接 BD ．

∵ 四边形 ABCD 是菱形，

∴ AD=AB ．

又 ∵∠ A=60 ° ，

∴△ ABD 是等边三角形，

∴ AD=BD ， ∠ ADB=60 ° ，

∴∠ DBE= ∠ A=60 °

∵∠ EDF=60 ° ，

∴∠ ADF= ∠ BDE ． ∵ 在 △ ADF 与 △ BDE 中， ，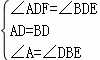

∴△ ADF ≌△ BDE （ ASA ），

∴ DF=DE ；

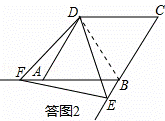
（ 2 ） DF=DE ．理由如下：

如答图 2 ，连接 BD ． ∵ 四边形 ABCD 是菱形，

∴ AD=AB ．

又 ∵∠ A=60 ° ，

∴△ ABD 是等边三角形，

∴ AD=BD ， ∠ ADB=60 ° ，

∴∠ DBE= ∠ A=60 °

∵∠ EDF=60 ° ，

∴∠ ADF= ∠ BDE ．

∵ 在 △ ADF 与 △ BDE 中， ，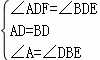

∴△ ADF ≌△ BDE （ ASA ），

∴ DF=DE ；

（ 3 ）由（ 2 ）知， △ ADF ≌△ BDE ．则 S _{△ ADF} =S _{△ BDE} ， AF=BE=x ．

依题意得： y=S _{△ BEF} +S _{△ ABD} = （ 2+x ） xsin60 ° + × 2 × 2sin60 ° = （ x+1 ） ² + ．即 y= （ x+1 ） ² + ．

∵ ＞ 0 ，

∴ 该抛物线的开口方向向上，

∴ 当 x=0 即点 E 、 B 重合时， y _最小值 = ．