早教吧作业答案频道 -->数学-->
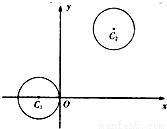
如图,在平面直角坐标系xOy中,已知圆,圆.(1)若过点C1(-1,0)的直线l被圆C2截得的弦长为,求直线l的方程;(2)设动圆C同时平分圆C1的周长、圆C2的周长.①证明:动
题目详情
如图,在平面直角坐标系xOy中,已知圆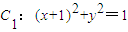 ,圆
,圆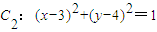 .
.
(1)若过点C 1 (-1,0)的直线l被圆C 2 截得的弦长为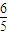 ,求直线l的方程;
,求直线l的方程;
(2)设动圆C同时平分圆C 1 的周长、圆C 2 的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
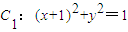 ,圆
,圆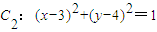 .
.(1)若过点C 1 (-1,0)的直线l被圆C 2 截得的弦长为
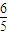 ,求直线l的方程;
,求直线l的方程;(2)设动圆C同时平分圆C 1 的周长、圆C 2 的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.

▼优质解答
答案和解析
分析:
(1)设过直线l方程:y=k(x+1),根据垂直于弦的直径的性质,结合点到直线的距离公式列式,可解出k的值,从而得到直线l的方程;(2)①由题意,圆心C到C1、C2两点的距离相等,由此结合两点间的距离公式建立关系式,化简整理得x+y-3=0,即为所求定直线方程;②根据题意设C(m,3-m),得到圆C方程关于参数m的一般方程形式,由此可得动圆C经过圆x2+y2-6y-2=0与直线x-y+1=0的交点,最后联解方程组,即可得到动圆C经过的定点坐标.
(1)设过点C1(-1,0)的直线l方程:y=k(x+1),化成一般式kx-y+k=0∵直线l被圆C2截得的弦长为,∴点C2(3,4)到直线l的距离为d==,解之得k=或由此可得直线l的方程为:4x-3y+4=0或3x-4y+3=0.(2)①设圆心C(x,y),由题意,得CC1=CC2,即=,化简整理,得x+y-3=0,即动圆圆心C在定直线x+y-3=0上运动.②设圆C过定点,设C(m,3-m),则动圆C的半径为=,于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,整理,得x2+y2-6y-2-2m(x-y+1)=0,由得或所以动圆C经过定点,其坐标为,.
点评:
本题求被定圆截得定长的弦所在直线方程,并探索动圆圆心在定直线上的问题.考查了直线与圆的方程、直线与圆和圆与圆的位置关系,考查学生运算能力.
分析:
(1)设过直线l方程:y=k(x+1),根据垂直于弦的直径的性质,结合点到直线的距离公式列式,可解出k的值,从而得到直线l的方程;(2)①由题意,圆心C到C1、C2两点的距离相等,由此结合两点间的距离公式建立关系式,化简整理得x+y-3=0,即为所求定直线方程;②根据题意设C(m,3-m),得到圆C方程关于参数m的一般方程形式,由此可得动圆C经过圆x2+y2-6y-2=0与直线x-y+1=0的交点,最后联解方程组,即可得到动圆C经过的定点坐标.
(1)设过点C1(-1,0)的直线l方程:y=k(x+1),化成一般式kx-y+k=0∵直线l被圆C2截得的弦长为,∴点C2(3,4)到直线l的距离为d==,解之得k=或由此可得直线l的方程为:4x-3y+4=0或3x-4y+3=0.(2)①设圆心C(x,y),由题意,得CC1=CC2,即=,化简整理,得x+y-3=0,即动圆圆心C在定直线x+y-3=0上运动.②设圆C过定点,设C(m,3-m),则动圆C的半径为=,于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,整理,得x2+y2-6y-2-2m(x-y+1)=0,由得或所以动圆C经过定点,其坐标为,.
点评:
本题求被定圆截得定长的弦所在直线方程,并探索动圆圆心在定直线上的问题.考查了直线与圆的方程、直线与圆和圆与圆的位置关系,考查学生运算能力.
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
在直角坐标系中,有一条长度为2的线段AB,点A在y轴上运动,点B在x轴上运动,且保持线段长度不变在 2020-05-16 …
在平面直角坐标系中,怎么由线段长度和一点坐标求另一点坐标?例如知道了点B(3,0),BP长度为2根 2020-06-14 …
全站仪已知轴线两端点坐标求轴线延长线上一点坐标条件:已知轴线两端点A和B的坐标,例如A(x=294 2020-06-14 …
关于斜二测画法画直观图说法不正确的是()A.在实物图中取坐标系不同,所得的直观图有可能不同B.平行 2020-06-27 …
关于斜二测画法画直观图说法不正确的是()A.在实物图中取坐标系不同,所得的直观图有可能不同B.平行 2020-06-27 …
线的一端栓一个小球,匀速圆周运动的一道题、线的一端栓一个小球,固定线的另一端,使球在水平面内做匀速 2020-06-29 …
根据条件求二次函数的解析式(1)抛物线过(-1,0),(3,0),(1,-5)三点(2)抛物线的顶 2020-07-01 …
在平面直角坐标系中点A的坐标为(40)一点A为圆心4为半径的圆与x轴交于OB两点P是x轴的一个动点 2020-07-26 …
如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物 2020-07-26 …
关于数学上的“坐标”坐标,在数学上有两个意义:1,有向线段基线的长度(有向线段的坐标又叫有向线段的 2020-08-02 …