已知函数f（x）满足f（-x）=f（x），f（x+8）=f（x），且当x∈（0，4]时f（x）=ln(2x)x，关于x的不等式f2（x）+af（x）>0在[-2016，2016]上有且只有2016个整数解，则实数a的取值范围是（）A.（

Question

已知函数f（x）满足f（-x）=f（x），f（x+8）=f（x），且当x∈（0，4]时f（x）=

(ln(2x))/(x)，关于x的不等式f²（x）+af（x）>0在[-2016，2016]上有且只有2016个整数解，则实数a的取值范围是（　　）

A. （-

(1)/(3)ln6，ln2]

B. （-ln2，-

(1)/(3)ln6）

C. （-ln2，-

(1)/(3)ln6]

D. （-

(1)/(3)ln6，ln2）

Answer 1

∵函数f（x）满足f（-x）=f（x），f（x+8）=f（x），
∴函数f（x）是偶函数，且周期是8，则在[-2016，2016]上共有504个周期，
∵不等式在[-2016，2016]上有且只有2016个整数解，∴在一个周期上有且只有4个整数解，
由偶函数的性质可得，在（0，4]上有且只有2个整数解，
∵当x∈（0，4]时f（x）=(ln(2x))/(x)，∴则f′（x）=(1-ln(2x))/(x2)，
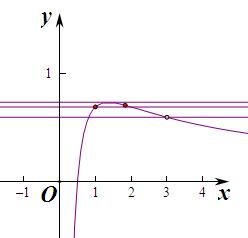
当f′（x）>0得1-ln（2x）>0，即ln（2x）<1，
即0<2x<e，即0<x<(e)/(2)，
由f′（x）<0得1-ln（2x）<0，得ln（2x）>1，
即2x>e，即x>(e)/(2)，
即当x=(e)/(2)时，函数f（x）取得极大值，同时也是最大值
f（(e)/(2)）=(lne)/((e)/(2))=(2)/(e)，
即当0<x<(e)/(2)时，f（x）<(2)/(e)有一个整数解1，
当x>(e)/(2)时，0<f（x）<(2)/(e)有无数个整数解，
①若a=0，则f²（x）+af（x）>0得f²（x）>0，此时有无数个整数解，不满足条件．
②若a>0，
则由f²（x）+af（x）>0得f（x）>0或f（x）<-a，
当f（x）>0时，不等式由无数个整数解，不满足条件．
③当a<0时，由f²（x）+af（x）>0得f（x）>-a或f（x）<0，
当f（x）<0时，没有整数解，
则要使当f（x）>-a有两个整数解，
∵f（1）=ln2，f（2）=(ln4)/(2)=ln2，f（3）=(ln6)/(3)，
∴当f（x）≥ln2时，函数有两个整数点1，2，当f（x）≥(ln6)/(3)时，函数有3个整数点1，2，3
∴要使f（x）>-a有两个整数解，
则(ln6)/(3)≤-a<ln2，即-ln2<a≤-(1)/(3)ln6，
故选：C．