早教吧作业答案频道 -->数学-->
等腰Rt△ABC中,AC=AB,∠BAC=90°,点A、点B分别是y轴、x轴上的两个动点.(1)如图1,若A(0,2),B(1,0),求C点的坐标;(2)如图2,当等腰Rt△ABC运动,直角边AC交x轴于点D,斜边BC交y轴
题目详情
等腰Rt△ABC中,AC=AB,∠BAC=90°,点A、点B分别是y轴、x轴上的两个动点.
(1)如图1,若A(0,2),B(1,0),求C点的坐标;
(2)如图2,当等腰Rt△ABC运动,直角边AC交x轴于点D,斜边BC交y轴于点E,且点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图3,在等腰Rt△ABC不断运动的过程中,直角边AC交x轴于点D,斜边BC交y轴于点E,若BD始终是∠ABC平分线,试探究:线段BD与OA+OD之间存在的数量关系,并说明理由.
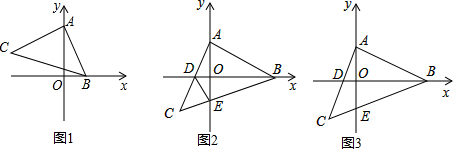
(1)如图1,若A(0,2),B(1,0),求C点的坐标;
(2)如图2,当等腰Rt△ABC运动,直角边AC交x轴于点D,斜边BC交y轴于点E,且点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图3,在等腰Rt△ABC不断运动的过程中,直角边AC交x轴于点D,斜边BC交y轴于点E,若BD始终是∠ABC平分线,试探究:线段BD与OA+OD之间存在的数量关系,并说明理由.

▼优质解答
答案和解析
(1)如图1,过点C作CF⊥y轴于点F,
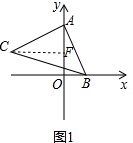
∵A(0,2),B(1,0),
∴OA=2,OB=1,
∵CF⊥y轴于点F,
∴∠CFA=90°,∠ACF+∠CAF=90°,
∵∠CAB=90°,
∴∠CAF+∠BAO=90°,
∴∠ACF=∠BAO,
在△ACF和△ABO中,
∴△ACF≌△ABO(AAS),
∴CF=OA=1,AF=OB=2
∴OF=1
∴C(-1,-1);
(2)如图2,过点C作CG⊥AC交y轴于点G,
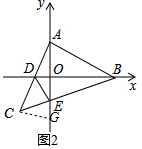
∵CG⊥AC,
∴∠ACG=90°,∠CAG+∠AGC=90°,
∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∴∠AGC=∠ADO,
在△ACG和△ABD中,
∴△ACG≌△ABD(AAS)
∴CG=AD=CD,∠ADB=∠G,
∵∠ACB=45°,∠ACG=90°,
∴∠DCE=∠GCE=45°,
在△DCE和△GCE中,
∴△DCE≌△GCE(SAS)
∴∠CDE=∠G,
∴∠ADB=∠CDE;
(3)如图3,在OB上截取OH=OD,连接AH,
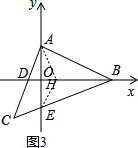
由对称性得AD=AH,∠ADH=∠AHD,
∴∠AHD=∠ADH=∠BAO=∠BEO,
∴∠AEC=∠BHA,
在△ACE和△BAH中,
∴△ACE≌△BAH(AAS)
∴AE=BH=2OA
∵DH=2OD,
∴BD=2(OA+OD).

∵A(0,2),B(1,0),
∴OA=2,OB=1,
∵CF⊥y轴于点F,
∴∠CFA=90°,∠ACF+∠CAF=90°,
∵∠CAB=90°,
∴∠CAF+∠BAO=90°,
∴∠ACF=∠BAO,
在△ACF和△ABO中,
|
∴△ACF≌△ABO(AAS),
∴CF=OA=1,AF=OB=2
∴OF=1
∴C(-1,-1);
(2)如图2,过点C作CG⊥AC交y轴于点G,

∵CG⊥AC,
∴∠ACG=90°,∠CAG+∠AGC=90°,
∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∴∠AGC=∠ADO,
在△ACG和△ABD中,
|
∴△ACG≌△ABD(AAS)
∴CG=AD=CD,∠ADB=∠G,
∵∠ACB=45°,∠ACG=90°,
∴∠DCE=∠GCE=45°,
在△DCE和△GCE中,
|
∴△DCE≌△GCE(SAS)
∴∠CDE=∠G,
∴∠ADB=∠CDE;
(3)如图3,在OB上截取OH=OD,连接AH,

由对称性得AD=AH,∠ADH=∠AHD,
∴∠AHD=∠ADH=∠BAO=∠BEO,
∴∠AEC=∠BHA,
在△ACE和△BAH中,
|
∴△ACE≌△BAH(AAS)
∴AE=BH=2OA
∵DH=2OD,
∴BD=2(OA+OD).
看了 等腰Rt△ABC中,AC=A...的网友还看了以下:
已知实数t满足关系式loga(t/a^3)=loga(y/a^3)(a>0且a≠1)(1)令t=a 2020-04-26 …
已知椭圆T的方程为x^2/a^2+y^2/b^2=1(a>b>0),A(0,b),B(0,-b)和 2020-04-27 …
谁能把我把这些公式弄成手写公式s(t)=at^2/2+v(0)t=(v(t)^2-v(0)^2)/ 2020-05-16 …
n阶方阵A对任意n维向量x,满足x^TAx=0,充要条件为AT=-A;证明:充分性:f=x^TAx 2020-05-17 …
r(A*A^T)=r(A^T*A)=r(A)证明方程AX=0与A^TAX=0同解AX=0显然有A^ 2020-06-10 …
设A为奇数阶实对称矩阵,且det(A)>0.求证:存在非零向量X,满足X∧T*A*X>0 2020-06-22 …
关于A=0的证明设A是n阶实对称矩阵,且A²=0证明A=0.其中一种证明方法是这样的:由A(T)A= 2020-11-03 …
用mathmetica求解常微分方程组的问题!急急急r=1,d=0.5,a=0.1,b=0.02,x 2021-01-04 …
函数f(x)的定义域为D,若满足如下两条件:①f(x)在D内是单调函数;②存在[m/2,n/2]是D 2021-01-04 …
已知Ax=0的通解,如何求矩阵A例如A是2*4的矩阵,其基础解系为a1=(1,3,0,2)^T,a2 2021-02-11 …