早教吧作业答案频道 -->数学-->
在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)写出CG与EG的数量关系,并说明理由.(2)若AD=12,AB=20,求CE的长.
题目详情
在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.
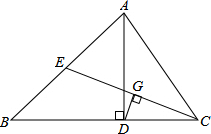
(1)写出CG与EG的数量关系,并说明理由.
(2)若AD=12,AB=20,求CE的长.

(1)写出CG与EG的数量关系,并说明理由.
(2)若AD=12,AB=20,求CE的长.
▼优质解答
答案和解析
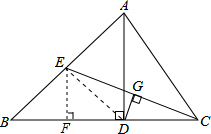 (1)CG=EG,
(1)CG=EG,
理由:连接ED,∵AD⊥BC
∴∠ADB=90°
∵CE是AB边上的中线
∴E是AB的中点
∴DE=
AB(直角三角形斜边上的中线等于斜边的一半)
又∵AE=
AB
∴AE=DE
∵AE=CD
∴DE=CD
即△DCE是等腰三角形,
∵DG⊥EC,
∴CG=EG;
(2)过点E作EF⊥BC于点F,
∵AD⊥BC,E为AB的中点,
∴EF
AD,
∴EF=6,
∵∠ADB=90°,AD=12,AB=20,
∴BD=16,
∴FD=BF=8,
∴ED=
=10,
∴DC=10,
∴EC=
=
=6
.
 (1)CG=EG,
(1)CG=EG,理由:连接ED,∵AD⊥BC
∴∠ADB=90°
∵CE是AB边上的中线
∴E是AB的中点
∴DE=
| 1 |
| 2 |
又∵AE=
| 1 |
| 2 |
∴AE=DE
∵AE=CD
∴DE=CD
即△DCE是等腰三角形,
∵DG⊥EC,
∴CG=EG;
(2)过点E作EF⊥BC于点F,
∵AD⊥BC,E为AB的中点,
∴EF
| ∥ |
. |
| 1 |
| 2 |
∴EF=6,
∵∠ADB=90°,AD=12,AB=20,
∴BD=16,
∴FD=BF=8,
∴ED=
| 62+82 |
∴DC=10,
∴EC=
| EF2+FC2 |
| 62+(8+10)2 |
| 10 |
看了 在△ABC中,AD是BC边上...的网友还看了以下:
将括号内字母发音相同的单词归类W(e)st,tr(a)ffic,(c)lass,t(e)le)l, 2020-05-14 …
G.U.A.G.E.L.A.N.组成什么英语 2020-05-17 …
●文法G=({E},{+,*,(,),a},P,E),其中P由下列产生式组成E->E+E|E*E|( 2020-05-25 …
文法G=({E},{+,*,(,),a},P,E),其中P由下列产生式组成E->E+E|E*E|(E 2020-05-26 …
文法G=({E),{+,*,(,),a},P,E),其中P由下列产生式组成E->E+E|E*E|(E 2020-05-26 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
高数导数问题.设f(x)=(e^x-e^a)g(x)在x=a处可导,则函数g(x)应该满足条件是? 2020-07-20 …
非空集合G关于运算○满足;1,对于任意a,b∈G,都有a○b∈G;2,存在e∈G,使对尤其是那个e 2020-08-01 …
三元一次方程组a*x+b*y+c*z+d=0,e*x+f*y+g*z+h=0,i*x+j*y+k* 2020-08-03 …
质量为m的物体,在距地面h高处以加速度a=g/2由静止开始竖直下落到地面.试分析这个过程中,机械能是 2020-11-02 …