早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.(1)求点B的坐标;(2)在点P的运动过
题目详情
如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
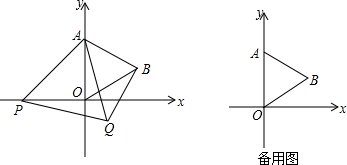
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.

▼优质解答
答案和解析
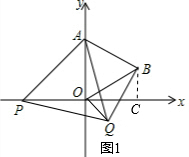 (1)如图1,过点B作BC⊥x轴于点C,
(1)如图1,过点B作BC⊥x轴于点C,
∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,OB=OA=2,
∴∠BOC=30°,而∠OCB=90°,
∴BC=
OB=1,OC=
,
∴点B的坐标为B(
,1);
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB,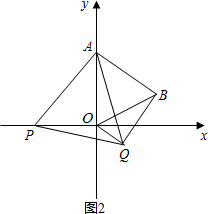
在△APO与△AQB中,
,
∴△APO≌△AQB(SAS),
∴∠ABQ=∠AOP=90°;
(3)当点P在x轴负半轴上时,点Q在点B的下方,
∵AB∥OQ,∠BQO=90°,∠BOQ=∠ABO=60°.
又OB=OA=2,可求得BQ=
,
由(2)可知,△APO≌△AQB,
∴OP=BQ=
,
∴此时P的坐标为(-
,0).
 (1)如图1,过点B作BC⊥x轴于点C,
(1)如图1,过点B作BC⊥x轴于点C,∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,OB=OA=2,
∴∠BOC=30°,而∠OCB=90°,
∴BC=
| 1 |
| 2 |
| 3 |
∴点B的坐标为B(
| 3 |
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB,

在△APO与△AQB中,
|
∴△APO≌△AQB(SAS),
∴∠ABQ=∠AOP=90°;
(3)当点P在x轴负半轴上时,点Q在点B的下方,
∵AB∥OQ,∠BQO=90°,∠BOQ=∠ABO=60°.
又OB=OA=2,可求得BQ=
| 3 |
由(2)可知,△APO≌△AQB,
∴OP=BQ=
| 3 |
∴此时P的坐标为(-
| 3 |
看了 如图,在平面直角坐标系中,已...的网友还看了以下:
春节的作文应该重点描写哪个方面,重点是哪个方面描写 2020-04-12 …
十万火急,在线等候(救命啊)areherebystatethatabove-mentionedca 2020-04-22 …
谈谈道德如何维持社会秩序请从各个方面考虑一下,是要用在思想道德修养的简答题上,希望能够深入一点,不 2020-05-16 …
已知两个圆锥,底面重合在一起,其中一个圆锥顶点到底面的距离为2cm,另一个圆锥顶点到底面的距离为3 2020-06-27 …
已知两个圆锥,底面重合在一起,其中一个圆锥顶点到底面的距离为2cm,另一个圆锥顶点到地面的距离为3 2020-06-27 …
依据调研,新能源汽车公用充电桩()A.a、c区的布局重点应在工业区B.b区布局重点在商业区、行政区 2020-06-29 …
“冯兰瑞老头”的冯老汉是个的人《百纳衣》1概括本文的中心2浓浓的母爱是本文表现的重点.在表现母爱时 2020-07-02 …
若两个平面互相平行,则分别在这两个平行平面内的直线为什么是平行或者异面?(重点解释一下为什么可以异面 2020-11-03 …
在定义地心坐标系时,起始大地子午面如何与起始天文子午面重合?在定义地心坐标系时,如果起始大地子午面与 2020-12-01 …
找个初中生谈谈我的学习方法我的学习态度不怎么样,史地生政治一般上课听得不太全面,我只有回家才去做笔记 2020-12-06 …