早教吧作业答案频道 -->数学-->
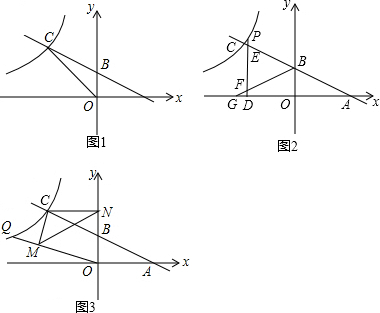
如图1,直线y=-12x+2交坐标轴于A,B两点,交双曲线y=kx(x<0)于点C,且S△AOC=8.(1)求k的值;(2)如图2,A,G关于y轴对称,P为双曲线上一点,过P作PD⊥x轴于D,分别交BG,AB于F,E.求证
题目详情
如图1,直线y=-
x+2交坐标轴于A,B两点,交双曲线y=
(x<0)于点C,且S△AOC=8.
(1)求k的值;
(2)如图2,A,G关于y轴对称,P为双曲线上一点,过P作PD⊥x轴于D,分别交BG,AB于F,E.求证:DE+DF=4;
(3)Q为双曲线上另一动点,连接OQ,过C作CM⊥OQ于M,CN⊥y轴于N,如图3,当Q点运动时,∠OMN是否为定值?猜想并证明你的结论.
| 1 |
| 2 |
| k |
| x |
(1)求k的值;
(2)如图2,A,G关于y轴对称,P为双曲线上一点,过P作PD⊥x轴于D,分别交BG,AB于F,E.求证:DE+DF=4;
(3)Q为双曲线上另一动点,连接OQ,过C作CM⊥OQ于M,CN⊥y轴于N,如图3,当Q点运动时,∠OMN是否为定值?猜想并证明你的结论.

▼优质解答
答案和解析
(1)对于直线y=-
x+2,当y=0时,x=4;当x=0时,y=2;
∴A(4,0),B(0,2),
设C(a,b),
∵S△COA=
×4×b=8,
∴b=4,
把C(a,4)代入y=-
x+2得:a=-4
∴C(-4,4),
把C(-4,4)代入y=
得:
k=-16,
(2)设P坐标为(m,n),
∵A,G关于y轴对称,且A(4,0),
∴G(-4,0),
∵B(0,2),
∴直线BG解析式为y=
x+2,
∵过P作PD⊥x轴于D,分别交BG于F,
∴F(m,
m+2),D(m,0)
∴DF=
m+2,
∵A(4,0),C(-4,4),
∴直线AC解析式为y=-
x+2,
∵过P作PD⊥x轴于D,分别交AC于E,
∴E(m,-
m+2),
∴DE=-
m+2,
∴DE+DF=-
m+2+=
m+2=4;
(3)当Q点运动时,∠OMN是定值.
理由:如图所示,
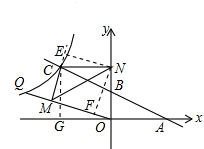
作NE⊥MC于E,作NF⊥OM于F,作CG⊥x轴于G;
则四边形CGON是正方形,∠CMF=∠MFN=∠NEM=90°,
∴四边形EMFN是矩形,CG=OG=ON=CN=4,∠OCN=∠CON=45°,
∵CM⊥OQ,CN⊥y轴,
∴∠CMO=∠CNO=90°,
∴C、M、O、N四点共圆,
∴∠OMN=∠OCN=45°.
当Q点运动时,∠OMN是定值,定值为45°.
| 1 |
| 2 |
∴A(4,0),B(0,2),
设C(a,b),
∵S△COA=
| 1 |
| 2 |
∴b=4,
把C(a,4)代入y=-
| 1 |
| 2 |
∴C(-4,4),
把C(-4,4)代入y=
| k |
| x |
k=-16,
(2)设P坐标为(m,n),
∵A,G关于y轴对称,且A(4,0),
∴G(-4,0),
∵B(0,2),
∴直线BG解析式为y=
| 1 |
| 2 |
∵过P作PD⊥x轴于D,分别交BG于F,
∴F(m,
| 1 |
| 2 |
∴DF=
| 1 |
| 2 |
∵A(4,0),C(-4,4),
∴直线AC解析式为y=-
| 1 |
| 2 |
∵过P作PD⊥x轴于D,分别交AC于E,
∴E(m,-
| 1 |
| 2 |
∴DE=-
| 1 |
| 2 |
∴DE+DF=-
| 1 |
| 2 |
| 1 |
| 2 |
(3)当Q点运动时,∠OMN是定值.
理由:如图所示,

作NE⊥MC于E,作NF⊥OM于F,作CG⊥x轴于G;
则四边形CGON是正方形,∠CMF=∠MFN=∠NEM=90°,
∴四边形EMFN是矩形,CG=OG=ON=CN=4,∠OCN=∠CON=45°,
∵CM⊥OQ,CN⊥y轴,
∴∠CMO=∠CNO=90°,
∴C、M、O、N四点共圆,
∴∠OMN=∠OCN=45°.
当Q点运动时,∠OMN是定值,定值为45°.
看了 如图1,直线y=-12x+2...的网友还看了以下:
2008年5月12日,我国四川省汶川地区发生8.O级大地震,造成重大财产损失和人员伤亡.为了确保大 2020-06-19 …
2008年5月12日14时28分,四川省汶川地区发生8.O级特大地震,给人民生命财产造成巨大损失。 2020-07-15 …
5月12日四川汶川发生了8.O级地震,许多房屋瞬时垮塌,几万人遇难……灾情牵动了党和国家领导人的心, 2020-11-12 …
5月12日四川汶川发生了8.O级地震,许多房屋瞬时垮塌,几万人遇难…灾情牵动了党和国家领导人的心,牵 2020-12-10 …
2008年北京时间5月12日14时28分,四川省汶川县发生里氏8.O级地震。地震发生后,国务院总理温 2020-12-10 …
2008年北京时间5月12日14时28分,四川省汶川县发生里氏8.O级地震。地震发生后,国务院总理温 2020-12-10 …
(2008•温州)2008年5月12日,四川汶川发生8.O级大地震.全国人民抗震救灾,众志成城.(1 2020-12-15 …
(2008•温州)2008年5月12日,四川汶川发生8.O级大地震.全国人民抗震救灾,众志成城.(1 2020-12-15 …
2008年5月12日,我国四川省汶川县发生了里氏8.O级特大地震,人员伤亡惨重.中国红十字会准备将5 2020-12-17 …
四川汶川发生8.O级地震,全国手机报在第一时间向手机用户发布了这一重大灾难事件。在震区这种特定的环境 2020-12-17 …