早教吧作业答案频道 -->数学-->
已知,∠ABC=90°,D是直线AB上的点,AD=BC.(1)过A作AF⊥AB截取AF=BD,连接DC,DF,CF,判断△CDF的形状;(2)E是直线BC上一点为CE=BD,AE,CD相交于点P,求∠APD.
题目详情
已知,∠ABC=90°,D是直线AB上的点,AD=BC.
(1)过A作AF⊥AB截取AF=BD,连接DC,DF,CF,判断△CDF的形状;
(2)E是直线BC上一点为CE=BD,AE,CD相交于点P,求∠APD.
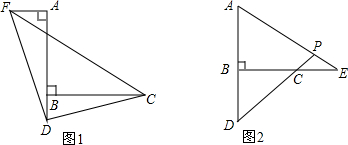
(1)过A作AF⊥AB截取AF=BD,连接DC,DF,CF,判断△CDF的形状;
(2)E是直线BC上一点为CE=BD,AE,CD相交于点P,求∠APD.

▼优质解答
答案和解析
(1)△CDF是等腰直角三角形,理由如下:
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
,
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形;
(2)作AF⊥AB于A,使AF=BD,连结DF,CF,如图,
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,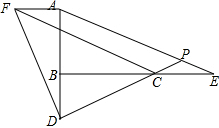
,
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形,
∴∠FCD=45°,
∵AF∥CE,且AF=CE,
∴四边形AFCE是平行四边形,
∴AE∥CF,
∴∠APD=∠FCD=45°.
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
|
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形;
(2)作AF⊥AB于A,使AF=BD,连结DF,CF,如图,
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,

|
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形,
∴∠FCD=45°,
∵AF∥CE,且AF=CE,
∴四边形AFCE是平行四边形,
∴AE∥CF,
∴∠APD=∠FCD=45°.
看了 已知,∠ABC=90°,D是...的网友还看了以下:
1.已有定义inta[10],*p;则正确的赋值语句是().A.p=100;B.p=a[5];C.p 2020-03-31 …
如果事件A,B满足.ACB则必有a.P(A)<P(B)b.P(A)>P(B)c.P(A)≤P(B) 2020-04-07 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),问新序列(F,H,C,D,P,A,M 2020-05-23 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),则新序列(F,H,C, D,P,A, 2020-05-23 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),问新序列(F,H,C,D,P,A,M 2020-05-23 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),问新序列(F, H,C,D,P,A, 2020-05-24 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),新序列(F, H,C,D,P,A,M 2020-05-24 …
设有字符序列(Q,H,C,Y,P,A, M, S, R, D, F, X),则新序列(F,H,C,D 2020-05-24 …
A.F,H,C,D,P,A,M,Q,R,S,Y,XB.P,A,C,S,Q,D,F,X,R,H,M,Y 2020-05-26 …
若有以下定义和赋值double*q,a=5.5;int*p,i=1;double*q,a=5.5; 2020-07-09 …