早教吧作业答案频道 -->数学-->
如图,O的半径为1,A,P,B,C是O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状:;(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于
题目详情
如图, O的半径为1,A,P,B,C是 O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状:___;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于
的什么位置时,四边形APBC的面积最大?求出最大面积.
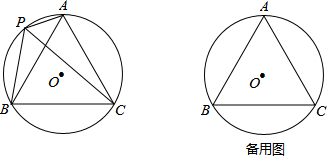
(1)判断△ABC的形状:___;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于
 |
| AB |

▼优质解答
答案和解析
证明:(1)△ABC是等边三角形.
证明如下:在 O中
∵∠BAC与∠CPB是
所对的圆周角,∠ABC与∠APC是
所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)在PC上截取PD=AP,如图1,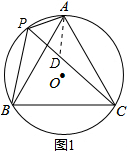
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP;
(3)当点P为
的中点时,四边形APBC的面积最大.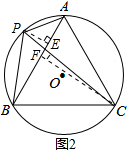
理由如下,如图2,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵S△APB=
AB•PE,S△ABC=
AB•CF,
∴S四边形APBC=
AB•(PE+CF),
当点P为
的中点时,PE+CF=PC,PC为 O的直径,
∴此时四边形APBC的面积最大.
又∵ O的半径为1,
∴其内接正三角形的边长AB=
,
∴S四边形APBC=
×2×
=
.
证明如下:在 O中
∵∠BAC与∠CPB是
 |
| BC |
 |
| AC |
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)在PC上截取PD=AP,如图1,

又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
|
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP;
(3)当点P为
 |
| AB |

理由如下,如图2,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵S△APB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形APBC=
| 1 |
| 2 |
当点P为
 |
| AB |
∴此时四边形APBC的面积最大.
又∵ O的半径为1,
∴其内接正三角形的边长AB=
| 3 |
∴S四边形APBC=
| 1 |
| 2 |
| 3 |
| 3 |
看了 如图,O的半径为1,A,P,...的网友还看了以下:
为下面句子中的加粗字选择正确解释(把答案的序号写在句后的括号里)。径A小路B径直,直接C直径D即, 2020-04-07 …
问一个初三几何题若要在直径为五十厘米的圆内作出四个相等的且直径最大宝的小圆,最大直径多少,精确到零 2020-04-25 …
在△ABC中,AB=5cm,BC=4cm,AC=3cm(1)若以C为圆心,2cm长为半径画⊙C,则 2020-04-26 …
如图所示,圆A半径1,圆B半径2,圆C半径3,两两外切,另有一红色小圆分别与此三圆外切,求红色小圆 2020-04-27 …
如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=45,点E是BC边上的动点,当以C 2020-05-13 …
急!高一物理:质量为m的小球从半径为R的四分之一圆轨道AB的最高点A静止滚下,最后落到地面上的C, 2020-05-13 …
O、A、B、C为空间四个点,又OA、OB、OC为空间的一个基底,则()A.O、A、B、C四点不共线 2020-05-14 …
在正方体ABCD—EFGH,有一个棱长为根号2的正四面体G-BDE,则正四面体的外接球半径为多少? 2020-05-16 …
先在决口岸上选用足够长度和梢径的马脚木,以每( )一组。A.二根B.三根C.四根D.五根 2020-05-28 …
492Q型发动机编号的含义足( )A.四缸,冲程为92mm的发动机B.四行程,缸径为92mm的发动机 2020-05-31 …