早教吧作业答案频道 -->数学-->
如图,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足|a+b|+(a-5)2=0(1)点A的坐标为,点B的坐标为;(2)如图,若点C的坐标为(-3,-2),且BE⊥AC于点E,OD⊥OC交BE延长线
题目详情
如图,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足|a+b|+(a-5)2=0
(1)点A的坐标为___,点B的坐标为___;
(2)如图,若点C的坐标为(-3,-2),且BE⊥AC于点E,OD⊥OC交BE延长线于D,试求点D的坐标;
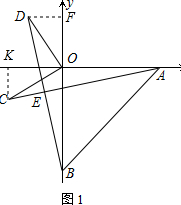
(3)如图,M、N分别为OA、OB边上的点,OM=ON,OP⊥AN交AB于点P,过点P作PG⊥BM交AN的延长线于点G,请写出线段AG、OP与PG之间的数列关系并证明你的结论.
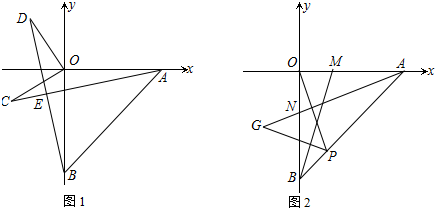
(1)点A的坐标为___,点B的坐标为___;
(2)如图,若点C的坐标为(-3,-2),且BE⊥AC于点E,OD⊥OC交BE延长线于D,试求点D的坐标;
(3)如图,M、N分别为OA、OB边上的点,OM=ON,OP⊥AN交AB于点P,过点P作PG⊥BM交AN的延长线于点G,请写出线段AG、OP与PG之间的数列关系并证明你的结论.

▼优质解答
答案和解析
 (1)∵|a+b|+(a-5)2=0,
(1)∵|a+b|+(a-5)2=0,
∴a=5,b=-5,
∴点A的坐标为(5,0),点B的坐标为
(0,-5),
故答案为:(5,0);(0,-5);
(2)过C作CK⊥x轴,过D作DF⊥y轴,
∵∠AED=∠BOK=90°,
∴∠DBO=∠OAC,
∵∠AOB+⊂BOC=∠BOK+∠BOC=90°+∠BOC,
∴∠AOC=∠BOD,
在△AOC与△DOB中,
,
∴△AOC≌△DOB(AAS),
∴OC=OD,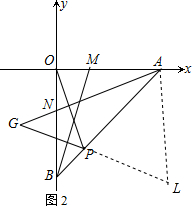
在△OCK与△ODF中,
,
∴△OCK≌△ODF,
∴DF=CK,OK=OF,
∴D(-2,3);
(3)延长GF到L,使PL=OP,连接AL,
在△AON与△BOM中,
,
∴△AON≌△BOM,
∴∠OAN=∠OBM,
∴∠MBA=∠NAB,
∵PG⊥BM,OP⊥AN,
∴∠NAB+∠OPA=∠MBA+∠GPB=90°,
∴∠OPA=∠GPB=∠APL,
在△OAP与△PAL中,
,
∴△OAP≌△PAL,
∴∠POA=∠L,∠OAP=∠PAL=45°,
∴∠OAL=90°,
∴∠POA=90°-∠POB,∠GAL=90°-∠OAN,
∵∠POB=∠OAN,
∴∠POA=∠GOL,
∴∠POA=∠GOL=∠L,
∴AG=GL,
∴AG=GL=GP+PL=GP+OP.
 (1)∵|a+b|+(a-5)2=0,
(1)∵|a+b|+(a-5)2=0,∴a=5,b=-5,
∴点A的坐标为(5,0),点B的坐标为
(0,-5),
故答案为:(5,0);(0,-5);
(2)过C作CK⊥x轴,过D作DF⊥y轴,
∵∠AED=∠BOK=90°,
∴∠DBO=∠OAC,
∵∠AOB+⊂BOC=∠BOK+∠BOC=90°+∠BOC,
∴∠AOC=∠BOD,
在△AOC与△DOB中,
|
∴△AOC≌△DOB(AAS),
∴OC=OD,

在△OCK与△ODF中,
|
∴△OCK≌△ODF,
∴DF=CK,OK=OF,
∴D(-2,3);
(3)延长GF到L,使PL=OP,连接AL,
在△AON与△BOM中,
|
∴△AON≌△BOM,
∴∠OAN=∠OBM,
∴∠MBA=∠NAB,
∵PG⊥BM,OP⊥AN,
∴∠NAB+∠OPA=∠MBA+∠GPB=90°,
∴∠OPA=∠GPB=∠APL,
在△OAP与△PAL中,
|
∴△OAP≌△PAL,
∴∠POA=∠L,∠OAP=∠PAL=45°,
∴∠OAL=90°,
∴∠POA=90°-∠POB,∠GAL=90°-∠OAN,
∵∠POB=∠OAN,
∴∠POA=∠GOL,
∴∠POA=∠GOL=∠L,
∴AG=GL,
∴AG=GL=GP+PL=GP+OP.
看了 如图,直线AB交x轴于点A(...的网友还看了以下:
如图,点D,E分别在线段AB和AC上,ADxAB=AExAC,点F是BE与CD的交点,求证三角形FD 2020-03-31 …
如图,点b.e.c.f在同一条直线上,be等于cf,ab平行于de,角a等于角d,证明三角形abc 2020-04-26 …
如图表示细胞内的四种大分子物质的结构层次(1)图中的E应为,能够贮存,A是,在生物体内共有种.(2 2020-05-02 …
(2011•揭阳模拟)读中国四大地理区域图,回答问题(1)A是我国的地区.B地区的自然环境特征是. 2020-05-13 …
根据右面人体血液循环和气体交换示意图,回答下列问题:(1)图中的G所指的是,内流静脉血;图中的E所 2020-05-13 …
如图,点D,E是线段AB的三等分点.(1)过D作DF‖BC交AC于F,过点E作EG‖BC交AC于G 2020-06-17 …
如图,点D,E在△ABC的边BC上,BD=CE,AD=AE,求证:AB=AC(不要用全等的解法) 2020-06-27 …
如图,点D,E分别在AB和AC上,DE//BC,角DBE=30度,角EBC=25度,求角BDE的度 2020-06-27 …
如图,点D,E,F分别在AB,BC,AC上,且DE∥AC,EF∥AB,说明∠A+∠B+∠C=180 2020-06-27 …
如图是青蛙的发育过程中某些阶段的示意图,请据图回答下列问题(1)青蛙发育的正确顺序是.(用图中的字 2020-06-30 …