早教吧作业答案频道 -->数学-->
已知关于x的一元二次方程x2+2x+k-12=0有实数根,k为正整数.(1)求k的值;(2)当此方程有两个非零的整数根时,将关于x的二次函数y=x2+2x+k-12的图象向下平移9个单位,求平移后的图象的表达
题目详情
已知关于x的一元二次方程x2+2x+
=0有实数根,k为正整数.
(1)求k的值;
(2)当此方程有两个非零的整数根时,将关于x的二次函数y=x2+2x+
的图象向下平移9个单位,求平移后的图象的表达式;
(3)在(2)的条件下,平移后的二次函数的图象与x轴交于点A,B(点A在点B左侧),直线y=kx+b(k>0)过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.
| k-1 |
| 2 |
(1)求k的值;
(2)当此方程有两个非零的整数根时,将关于x的二次函数y=x2+2x+
| k-1 |
| 2 |
(3)在(2)的条件下,平移后的二次函数的图象与x轴交于点A,B(点A在点B左侧),直线y=kx+b(k>0)过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.
▼优质解答
答案和解析
(1)∵关于x的一元二次方程x2+2x+
=0有实数根,
∴△=b2-4ac=4-4×
≥0,
∴k-1≤2,
∴k≤3,
∵k为正整数,
∴k的值是1,2,3;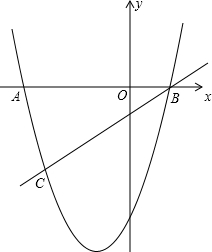
(2)∵方程有两个非零的整数根,
当k=1时,x2+2x=0,不合题意,舍去,
当k=2时,x2+2x+
=0,
方程的根不是整数,不合题意,舍去,
当k=3时,x2+2x+1=0,
解得:x1=x2=-1,符合题意,
∴k=3,
∴y=x2+2x+1,
∴平移后的图象的表达式y=x2+2x+1-9=x2+2x-8;
(3)令y=0,x2+2x-8=0,
∴x1=-4,x2=2,
∵与x轴交于点A,B(点A在点B左侧),
∴A(-4,0),B(2,0),
∵直线l:y=kx+b(k>0)经过点B,
∴函数新图象如图所示,当点C在抛物线对称轴左侧时,新函数的最小值有可能大于-5,
令y=-5,即x2+2x-8=-5,
解得:x1=-3,x2=1,(不合题意,舍去),
∴抛物线经过点(-3,-5),
当直线y=kx+b(k>0)经过点(-3,-5),(2,0)时,
可求得k=1,
由图象可知,当0<k<1时新函数的最小值大于-5.
| k-1 |
| 2 |
∴△=b2-4ac=4-4×
| k-1 |
| 2 |
∴k-1≤2,
∴k≤3,
∵k为正整数,
∴k的值是1,2,3;

(2)∵方程有两个非零的整数根,
当k=1时,x2+2x=0,不合题意,舍去,
当k=2时,x2+2x+
| 1 |
| 2 |
方程的根不是整数,不合题意,舍去,
当k=3时,x2+2x+1=0,
解得:x1=x2=-1,符合题意,
∴k=3,
∴y=x2+2x+1,
∴平移后的图象的表达式y=x2+2x+1-9=x2+2x-8;
(3)令y=0,x2+2x-8=0,
∴x1=-4,x2=2,
∵与x轴交于点A,B(点A在点B左侧),
∴A(-4,0),B(2,0),
∵直线l:y=kx+b(k>0)经过点B,
∴函数新图象如图所示,当点C在抛物线对称轴左侧时,新函数的最小值有可能大于-5,
令y=-5,即x2+2x-8=-5,
解得:x1=-3,x2=1,(不合题意,舍去),
∴抛物线经过点(-3,-5),
当直线y=kx+b(k>0)经过点(-3,-5),(2,0)时,
可求得k=1,
由图象可知,当0<k<1时新函数的最小值大于-5.
看了 已知关于x的一元二次方程x2...的网友还看了以下:
已知x,y是实数,且y=根号x平方-9加上根号9-x平方/x+3加7,求xy的平方根 2020-04-11 …
英语作文100词用英语描述成龙,100词,最好初一水平的.我实在编不出100词啊. 2020-04-11 …
设方程1996平方x平方-1995*1997x-1=0的较大实根为p,而方程x平方+1996x-1 2020-04-27 …
已知实数x,y满足2x的平方+6xy+9y的平方-2x+1=0,试求x,y的值实数x,y满足2x^ 2020-05-15 …
基本事实若ab=0 则a=0或b=0 一元二次方程x的平方-x-2=0可通过因式分解化为(x-2) 2020-05-16 …
设集合A={x-y,x+y,xy},B={x平方+y平方,x平方-y平方,0}.若A=B,球实数x 2020-05-16 …
已知关于x的一元二次方程x的平方x²=2(1-m)x-m²的两实数根为x1,x2,q已知关于x的一 2020-05-16 …
已知关于X的方程X的平方减去(2K-3)X+K的平方+1=0若此方程的两实数根X1和X2满足已知关 2020-05-16 …
研究平抛运动的实验.记录小球轨迹的白纸上,记录了竖直向下的y轴方向和水平的x轴方向以及轨迹上三个点 2020-05-17 …
f(x)=a的x平方(a>0,a≠1)在区间[0,1]上的最大值与最小值的和为3,则实数a的值.f 2020-05-23 …