在矩形ABCD中，AB=3，AD=4，动点Q从点A出发，以每秒1个单位的速度，沿AB向点B移动；同时点P从点B出发，仍以每秒1个单位的速度，沿BC向点C移动，连接QP，QD，PD．若两个点同时运动的时间为x秒

Question

在矩形ABCD中，AB=3，AD=4，动点Q从点A出发，以每秒1个单位的速度，沿AB向点B移动；同时点P从点B出发，仍以每秒1个单位的速度，沿BC向点C移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0<x≤3），解答下列问题：

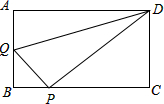
（1）设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最大值？并求出最小值；
（2）是否存在x的值，使得QP⊥DP？试说明理由．

Answer 1

（1）∵四边形ABCD为矩形，
∴BC=AD=4，CD=AB=3，
当运动x秒时，则AQ=x，BP=x，
∴BQ=AB-AQ=3-x，CP=BC-BP=4-x，
∴S_△ADQ=(1)/(2)AD•AQ=(1)/(2)×4x=2x，S_△BPQ=(1)/(2)BQ•BP=(1)/(2)（3-x）x=(3)/(2)x-(1)/(2)x²，S_△PCD=(1)/(2)PC•CD=(1)/(2)•（4-x）•3=6-(3)/(2)x，
又S_矩形ABCD=AB•BC=3×4=12，
∴S=S_矩形ABCD-S_△ADQ-S_△BPQ-S_△PCD=12-2x-（(3)/(2)x-(1)/(2)x²）-（6-(3)/(2)x）=(1)/(2)x²-2x+6=(1)/(2)（x-2）²+4，
即S=(1)/(2)（x-2）²+4，
∴S为开口向上的二次函数，且对称轴为x=2，
∴当0<x<2时，S随x的增大而减小，当2<x≤3时，S随x的增大而增大，
又当x=0时，S=5，当S=3时，S=(9)/(2)，但x的范围内取不到x=0，
∴S不存在最大值，当x=2时，S有最小值，最小值为4；
（2）存在，理由如下：
由（1）可知BQ=3-x，BP=x，CP=4-x，
当QP⊥DP时，则∠BPQ+∠DPC=∠DPC+∠PDC，
∴∠BPQ=∠PDC，且∠B=∠C，
∴△BPQ∽△CDP，
∴(BQ)/(PC)=(BP)/(CD)，即(3-x)/(4-x)=(x)/(3)，解得x=(7+√(13))/(2)（舍去）或x=(7-√(13))/(2)，
∴当x=

7-

作业帮用户 2017-02-10

问题解析

（1）可用x表示出AQ、BQ、BP、CP，从而可表示出S_△ADQ、S_△BPQ、S_△PCD的面积，则可表示出S，再利用二次函数的增减性可求得是否有最大值，并能求得其最小值；
（2）用x表示出BQ、BP、PC，当QP⊥DP时，可证明△BPQ∽△CDP，利用相似三角形的性质可得到关于x的方程，可求得x的值．

名师点评

本题考点：

四边形综合题

考点点评：

本题为四边形的综合应用，涉及知识点有矩形的性质、二次函数的最值、相似三角形的判定和性质及方程思想等．在（1）中求得S关于x的关系式后，求S的最值时需要注意x的范围，在（2）中证明三角形相似是解题的关键．本题考查知识点较多，综合性较强，难度适中．

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议