早教吧作业答案频道 -->数学-->
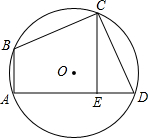
如图,四边形ABCD内接于O,∠BAD=90°,BC=CD,过点C作CE⊥AD,垂足为E,若AE=3,DE=3,求∠ABC的度数.
题目详情
如图,四边形ABCD内接于 O,∠BAD=90°,
=
,过点C作 CE⊥AD,垂足为E,若AE=3,DE=
,求∠ABC的度数.
 |
| BC |
 |
| CD |
| 3 |

▼优质解答
答案和解析
作BF⊥CE于F,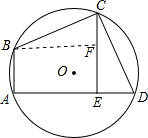
∵∠BCF+∠DCE=90°,∠D+∠DCE=90°,
∴∠BCF=∠D.
又BC=CD,
∴Rt△BCF≌Rt△CDE.
∴BF=CE.
又∵∠BFE=∠AEF=∠A=90°,
∴四边形ABFE是矩形.
∴BF=AE.
∴AE=CE=3,
在Rt△CDE中
∵tan∠D=
=
∴∠D=60°
∵∠ABC+∠D=180°
∴∠ABC=120°.

∵∠BCF+∠DCE=90°,∠D+∠DCE=90°,
∴∠BCF=∠D.
又BC=CD,
∴Rt△BCF≌Rt△CDE.
∴BF=CE.
又∵∠BFE=∠AEF=∠A=90°,
∴四边形ABFE是矩形.
∴BF=AE.
∴AE=CE=3,
在Rt△CDE中
∵tan∠D=
| CE |
| DE |
| 3 |
∴∠D=60°
∵∠ABC+∠D=180°
∴∠ABC=120°.
看了 如图,四边形ABCD内接于O...的网友还看了以下:
1.-2的相反数是.2.已知∠A=30°,则∠A的补角是度.3.分解因式:=.4.化简:=.5.点 2020-05-04 …
2012年10月14日,奥地利著名极限运动员费利克斯・鲍姆加特纳在美国新墨西哥州上空,从距地面高度 2020-06-10 …
一年级学生8人,每人在两种不同条件下接受某种技能训练,在三次练习中共发生的错误量如下:(A种条件) 2020-06-10 …
奥地利著名极限运动员鲍姆加特纳曾经从距地面高度约3.9万米的高空跳下,并成功着陆,一举打破多项世界 2020-07-04 …
2012年10月14日极限运动员鲍姆加特纳从距地面高度约3.9万米的氦气球携带的太空舱上跳下并成功 2020-07-08 …
与算式0.39×1.26的积相等的式子是()A.3.9×12.6B.39×0.126C.0.039 2020-07-18 …
先将下面的式子化成同底数幂的形式,然后再计算.3×9×27×81×243×729. 2020-07-19 …
用简便方法计算下面各题8.7×0.72+0.28×8.7+8.3.9×9.9+3.91.25×88 2020-07-19 …
2011年东莞市约有38500名应届毕业生参加中考,按四舍五入保留两位有效数字,38500用科学记数 2020-11-12 …
(2009•宜昌)用简便方法计算.3.9×45+7.1×80%-0.83.9÷(1.3×5)199× 2020-11-12 …