早教吧作业答案频道 -->数学-->
在直角坐标平面中,△ABC的两个顶点A,B的坐标分别为A(-1,0)B(1,0),平面内两点G,M同时满足下列条件:①++=;②||=||=||;③∥.(1)求△ABC的顶点C的轨迹方程;(2)过点P(3,0
题目详情
在直角坐标平面中,△ABC的两个顶点A,B的坐标分别为A(-1,0)B(1,0),平面内两点G,M同时满足下列条件:①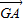 +
+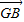 +
+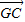 =
=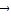 ;②|
;②|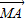 |=|
|=|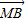 |=|
|=|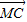 |;③
|;③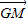 ∥
∥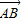 .
.
(1)求△ABC的顶点C的轨迹方程;
(2)过点P(3,0)的直线l与(1)中轨迹交于不同的两点E,F,求△OEF面积的最大值.
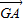 +
+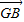 +
+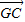 =
=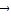 ;②|
;②|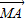 |=|
|=|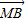 |=|
|=|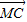 |;③
|;③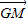 ∥
∥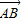 .
.(1)求△ABC的顶点C的轨迹方程;
(2)过点P(3,0)的直线l与(1)中轨迹交于不同的两点E,F,求△OEF面积的最大值.
▼优质解答
答案和解析
【答案】分析:(1)分别设出点C、G、M的坐标,利用条件||=||求出M的横坐标,结合∥可得G和M的纵坐标相等,然后利用把G和M的坐标用C的坐标表示,代入||=||即可得到C的轨迹方程;(2)设出直线l的方程,和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系得到E、F两点的横坐标的和与积,写出面积后得到关于直线斜率k的表达式,利用换元法降幂,然后利用导数求最值.(1)设C(x,y),G(x,y),M(xM,yM).∵,∴M点在线段AB的中垂线上.由已知A(-1,0),B(1,0),∴xM=0.又∵,∴yM=y.又,∴(-1-x,-y)+(1-x,-y)+(x-x,y-y)=(0,0)∴,∴. ∵|MB|=|MC|,∴,∴(y≠0),∴顶点C轨迹方程为(y≠0).(2)设直线l方程为:y=k(x-3)(k≠0),E(x1,y1),F(x2,y2),由,消去y得:(k2+3)x2-6k2x+9k2-3=0 ①∴,. 由方程①知△=(6k2)2-4(k2+3)(9k2-3)>0,∴k2<,∵k≠0,∴0<k2<. 而==.令k2=t,则,.记,求导后可得当时△OEF面积有最大值为.点评:本题考查了向量在几何中的应用,是直线与圆锥曲线的综合题,训练了“设而不求”的解题思想方法,训练了换元法,考查了导数在求最值中的作用,该题涉及条件多,解答的关键是找准入手点,是有一定难度题目.
看了 在直角坐标平面中,△ABC的...的网友还看了以下:
如图,在平面直角坐标系中,直线AB.CD分别与x轴、y轴交与A.B.C.D,点A(-2,0),B( 2020-05-15 …
已知在平面直角坐标系中直线AB,CD分别与X轴,Y轴交于A,B,C,D,点A(-2,0)B(0,3 2020-05-15 …
如图AC垂直于BC,CD垂直于AB,角1=角2,则下列结论中正确的有()①角1=角B②角3=角A③ 2020-05-17 …
1、在△ABC中 已知A=π/3 a=√3 b=1 解三角形 2、a=4 b=4√3 A=30°解 2020-06-27 …
已知a=10000,b=9999,求a^2+b^2-2ab-6a+6b+92.已知a,b,c为三角 2020-07-19 …
已知角1是锐角,角2是钝角,角3是直角,请问角1,角2,角3的大小关系是().A角1>角2>角3, 2020-07-30 …
以点O位位似中心,在方格图中将三角形ABC放大为原来的两倍,得到三角形A‘B’C‘,A(0,1)B 2020-08-02 …
整式综合1.求[8+2(k-1)][60-3(k-1)]的最小值.2.已知1/(a-b)+1/(b- 2020-10-31 …
在三角型abc中.若角a=2角b10度.角b=2角c-10度.则角a=?在△ABC中:(1)若∠A= 2020-10-31 …
适合条件∠A=∠B=1/3∠C的三角形一定是()A.锐角三角形B.钝角三角形C.直角三角形D.任意三 2020-12-05 …