早教吧作业答案频道 -->数学-->
在矩形ABCD中,AD=8,AB=6,点E为射线DC上一个动点,把△ADE沿AE折叠,使点D落在点F处,若△CEF为直角三角形时,DE的长为.
题目详情
在矩形ABCD中,AD=8,AB=6,点E为射线DC上一个动点,把△ADE沿AE折叠,使点D落在点F处,若△CEF为直角三角形时,DE的长为___.

▼优质解答
答案和解析
 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠D=∠B=90°,CD=AB=6,
∴AC=
=
=10,
当△CEF为直角三角形时,有两种情况:
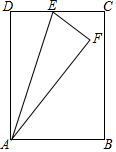
①当点F落在矩形内部时,F落在AC上,如图1所示.
由折叠的性质得:EF=DE,AF=AD=8,
设DE=x,则EF=x,CE=6-x,
∴CE=6-x,
在Rt△CEF中,由勾股定理得:
∵EF2+CF2=CE2,
∴x2+22=(6-x)2,
解得x=
,
∴DE=
;
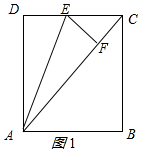
②当点F落在AB边上时,如图2所示.
此时ADEF为正方形,
∴DE=AD=8.
综上所述,BE的长为
或8.
故答案为:
或8.
 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,∴∠D=∠B=90°,CD=AB=6,
∴AC=
| AD2+CD2 |
| 82+62 |
当△CEF为直角三角形时,有两种情况:
①当点F落在矩形内部时,F落在AC上,如图1所示.
由折叠的性质得:EF=DE,AF=AD=8,
设DE=x,则EF=x,CE=6-x,
∴CE=6-x,
在Rt△CEF中,由勾股定理得:
∵EF2+CF2=CE2,

∴x2+22=(6-x)2,
解得x=
| 8 |
| 3 |
∴DE=
| 8 |
| 3 |
②当点F落在AB边上时,如图2所示.
此时ADEF为正方形,
∴DE=AD=8.
综上所述,BE的长为
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
看了 在矩形ABCD中,AD=8,...的网友还看了以下:
如图所示,在△ABC中,AD是BC边如图所示,在△ABC中,AD是BC边上的中线,延长AD到E,使 2020-04-09 …
在梯形ABCD中,AD平行CD AD=BC 点M.N为AD.BC的中点 CE垂直AB于E 若AE= 2020-05-16 …
已知:如图,在△ABC中,AD,BE分别是BC,AC边上的高,AD,BE相交于点F.求证:△AEF 2020-06-02 …
如图(1),在△ABC中,AB=AC,∠A=36°.(1)直接写出∠ABC的度数;(2)如图(2) 2020-06-02 …
如图,在△ABC中,AD平∠BAC,CE⊥AD于点O,EF‖BC,求证EC平分∠FED如图,在△A 2020-06-27 …
8、如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.⑴ 2020-06-27 …
如图,在△ABC中,AD平分∠BAC,P为线段AD上一个动点,PE⊥AD交直线BC于点E①若∠B= 2020-06-27 …
有一块金属,在空中称得重3.8牛顿,将它浸没在盛满水的溢水杯中时,有50毫升的水从溢水杯中流入量筒 2020-07-05 …
如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋 2020-07-17 …
在△ABC中AD是∠BAC的外角平分线在△ABC中,AD是∠BAC的外角平分线,P是线段AD上异于 2020-07-22 …