早教吧作业答案频道 -->数学-->
已知如图:二次函数y=x2-2x-3,根据图象回答下列问题:(1)设函数图象与x轴交于A、B两点(A在B的左边),与y轴交于点C,求△ABC的面积.(2)在抛物线的对称轴上找一点P,使PA+PC最小,求
题目详情
已知如图:二次函数y=x2-2x-3,根据图象回答下列问题:
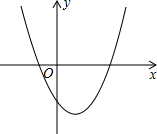
(1)设函数图象与x轴交于A、B两点(A在B的左边),与y轴交于点C,求△ABC的面积.
(2)在抛物线的对称轴上找一点P,使PA+PC最小,求出点P的坐标.
(3)若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形,使得正方形的一边在x轴上,其对边的两个端点在抛物线上,试求出这个最大正方形的边长.
(4)翻折x轴下方的图象,在形成的新图象中,当直线y=x+b与新图象有三个交点时,则b的值为___.

(1)设函数图象与x轴交于A、B两点(A在B的左边),与y轴交于点C,求△ABC的面积.
(2)在抛物线的对称轴上找一点P,使PA+PC最小,求出点P的坐标.
(3)若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形,使得正方形的一边在x轴上,其对边的两个端点在抛物线上,试求出这个最大正方形的边长.
(4)翻折x轴下方的图象,在形成的新图象中,当直线y=x+b与新图象有三个交点时,则b的值为___.
▼优质解答
答案和解析
如图1所示:
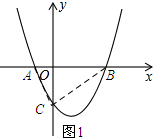
∵令x=0,得y=-3,
∴OC=3.
∵令y=0得:x2-2x-3=0,解得:x1=3,x2=-1,
∴A(-1,0)、B(3,0).
∴AB=4.
∴△ABC的面积=
AB•OC=
×4×3=6.
(2)如图2所示:连接BC,交抛物线的对称轴与点P,连接AP.
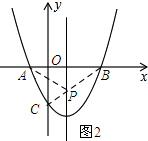
∵x=-
,
∴抛物线的对称轴为x=1.
∵点A与点B关于x=1对称,
∴PA=PB.
∴PA+PC=PB+PC.
当点C、P、B在一条直线上时,PA+PC有最小值.
设BC的解析式为y=kx+b,将点B、C的坐标代入得:
解得:k=1,b=-3.
∴直线BC的解析式为y=x-3.
将x=1代入得:y=1-3=-2.
∴P(1,-2).
(3)如图所示:
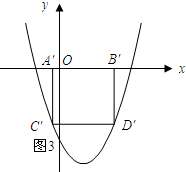
设点C′的坐标为(x,x2-2x-3).
∵点C′与D′关于x=1对称,
∴点D′的横坐标为2-x.
∴C′D′=2-2x.
∵四边形A′B′D′C′是正方形,
∴A′C′=C′D′.
∴2-2x=-(x2-2x-3).
解得:x1=2-
,x2=2+
(舍去),
∴C′D′=
.
∴正方形的面积为5.
(4)如图4所示,当直线y=x+b经过点A时.
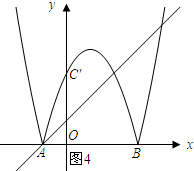
将A(-1,0)代入直线的解析式得:-1+b=0,解得:b=1.
如图5所示:
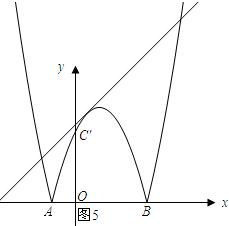
设经过点A、B、C′的抛物线的解析式为y=a(x+1)(x-3),将点C′的坐标代入得:-3a=3,解得a=-1.
∵a=-1,
∴抛物线的解析式为y=-x2+2x+3.
将y=-x2+2x+3与y=x+b联立得:-x2+2x+3=x+b.
∵直线y=x+b与抛物线y=-x2+2x+3有一个公共点,
∴方程x2-x+b-3=0判别式为0.
∴12-4×1×(b-3)=0.
解得:b=
.
综上所述,当b=1或b=
时,直线y=x+b与先函数图象有3个交点.
故答案为:1或
.

∵令x=0,得y=-3,
∴OC=3.
∵令y=0得:x2-2x-3=0,解得:x1=3,x2=-1,
∴A(-1,0)、B(3,0).
∴AB=4.
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图2所示:连接BC,交抛物线的对称轴与点P,连接AP.

∵x=-
| b |
| 2a |
∴抛物线的对称轴为x=1.
∵点A与点B关于x=1对称,
∴PA=PB.
∴PA+PC=PB+PC.
当点C、P、B在一条直线上时,PA+PC有最小值.
设BC的解析式为y=kx+b,将点B、C的坐标代入得:
|
解得:k=1,b=-3.
∴直线BC的解析式为y=x-3.
将x=1代入得:y=1-3=-2.
∴P(1,-2).
(3)如图所示:

设点C′的坐标为(x,x2-2x-3).
∵点C′与D′关于x=1对称,
∴点D′的横坐标为2-x.
∴C′D′=2-2x.
∵四边形A′B′D′C′是正方形,
∴A′C′=C′D′.
∴2-2x=-(x2-2x-3).
解得:x1=2-
| 5 |
| 5 |
∴C′D′=
| 5 |
∴正方形的面积为5.
(4)如图4所示,当直线y=x+b经过点A时.

将A(-1,0)代入直线的解析式得:-1+b=0,解得:b=1.
如图5所示:

设经过点A、B、C′的抛物线的解析式为y=a(x+1)(x-3),将点C′的坐标代入得:-3a=3,解得a=-1.
∵a=-1,
∴抛物线的解析式为y=-x2+2x+3.
将y=-x2+2x+3与y=x+b联立得:-x2+2x+3=x+b.
∵直线y=x+b与抛物线y=-x2+2x+3有一个公共点,
∴方程x2-x+b-3=0判别式为0.
∴12-4×1×(b-3)=0.
解得:b=
| 13 |
| 4 |
综上所述,当b=1或b=
| 13 |
| 4 |
故答案为:1或
| 13 |
| 4 |
看了 已知如图:二次函数y=x2-...的网友还看了以下:
下列不是反比例函数图象的特点的是()A.图象是由两部分构成B.图象与坐标轴无交点C.图象要么总向右 2020-04-08 …
(2012•松北区一模)已知反比例函数y=−1x,下列结论不正确的是()A.图象必经过点(一l,2 2020-04-08 …
3.3x-7≥4x-4的解是[ ] A.x≥3; B.x≤3; C.x≥-3; D.3.3x-7≥ 2020-05-16 …
已知集合U={x|x>0},C∪A={x|0<x<2},那么集合A=()A.{x|x≤0或x≥2} 2020-05-17 …
1.设P={x|x<1},Q={x|x2<4},则P∩Q()A.{x|-1<x<2}B.{x1.设 2020-06-05 …
23.中国画中,常用梅、兰、竹、菊来表示人格,这种方式涉及的意象类型是.A.仿象B.兴象C.喻象1 2020-06-20 …
有人做了如下试验:迅速将一只椿象杀死,尽管做得干净无声,也能引起其他椿象的逃避.椿象间的联系方式是 2020-07-05 …
有人做了如下试验:迅速将一只椿象杀死,尽管做的干净无声,也能引起其他椿象的逃逸。椿象间的联系方式是 2020-07-05 …
若点P的横坐标与纵坐标互为相反数,则点P一定在()A.原点B.第一、三象限两轴夹角的平分线上C.x 2020-08-01 …
以下结论正确的是()A.终边相同的角一定相等B.第一象限的角都是锐角C.x轴上的角均可表示为2kπ 2020-08-03 …