早教吧作业答案频道 -->数学-->
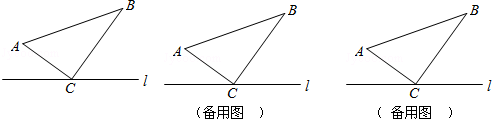
如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和2cm的运动速度同时开始运动
题目详情
如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和2cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动.
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,直线PQ能否把原三角形的周长分成相等的两部分?若能,请求出运动时间;若不能,请说明理由.
(3)在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,直线PQ能否把原三角形的周长分成相等的两部分?若能,请求出运动时间;若不能,请说明理由.
(3)在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.

▼优质解答
答案和解析
(1)如图1,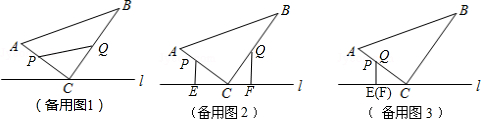
AP=2×1=2(cm),BQ=2×2=4(cm),
CP=6cm-2cm=4cm,CQ=8cm-4cm=4cm
PQ=
=4
(cm);
(2)直线PQ能把原三角形的周长分成相等的两部分,设此时时间为t秒,
理由是:由勾股定理得:AB=
=10(cm),
即△ABC的周长为6cm+8cm+10cm,
∵PQ把△ABC的周长分成相等的两部分,
∴6-t+8-2t=12,
解得:t=
,
即当t=
秒时,直线PQ把原三角形的周长分成相等的两部分;
(3)如图2,
∵△PEC与△QFC全等,
∴PC=QC.
∴6-t=8-2t.
解得:t=2;
如图3,
∵点P与点Q重合,
∴△PEC与△QFC全等,
∴6-t=2t-8.
解得:t=
.
综上所述:点P运动时间为2秒或
秒时,△PEC与△QFC全等.

AP=2×1=2(cm),BQ=2×2=4(cm),
CP=6cm-2cm=4cm,CQ=8cm-4cm=4cm
PQ=
| 42+42 |
| 2 |
(2)直线PQ能把原三角形的周长分成相等的两部分,设此时时间为t秒,
理由是:由勾股定理得:AB=
| 62+82 |
即△ABC的周长为6cm+8cm+10cm,
∵PQ把△ABC的周长分成相等的两部分,
∴6-t+8-2t=12,
解得:t=
| 2 |
| 3 |
即当t=
| 2 |
| 3 |
(3)如图2,
∵△PEC与△QFC全等,
∴PC=QC.
∴6-t=8-2t.
解得:t=2;
如图3,
∵点P与点Q重合,
∴△PEC与△QFC全等,
∴6-t=2t-8.
解得:t=
| 14 |
| 3 |
综上所述:点P运动时间为2秒或
| 14 |
| 3 |
看了 如图,△ABC中,∠ACB=...的网友还看了以下:
如图为人血液循环示意图,若在下肢静脉注射药物,则药物流经心脏各腔的先后顺序是()A.A→B→C→D 2020-05-13 …
一质量为1kg的小球,从半径为1m的14光滑圆弧轨道上端A点由静止开始滚下,再从轨道末端B点水平抛 2020-05-16 …
在狭义相对论中,下列说法中哪些是正确的A.一切运动物体相对于观察者的速度都不能大于真空中的光速.B 2020-06-19 …
已知二面角α-l-β的大小为50°,b、c是两条异面直线,则下面的四个条件中,一定能使b和c所成的 2020-06-27 …
在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列关系式中错误的是()A 2020-07-15 …
已知二次三项式x2+bx+c分解因式为(x-3)(x+1),则b,c的值为()A.b=-3,c=1 2020-07-31 …
点P为互相垂直的直线a、b外一点,过点P分别画直线c、d,使c∥a、d⊥a,那么下列判断中正确的是 2020-08-01 …
读下列四图,若只考虑昼夜和云量情况,下列气温排序正确的是A.a>b>c>dB.b>a>c>dC.c> 2020-12-05 …
下图为胸腔和肺的示意图,当肋间外肌和隔肌舒张时,图中三部位压力由大到小的顺序是()A.c>b>aB. 2020-12-06 …
(2013•永昌县)如图是在平行线间的五个图形,它们的面积相比较()A.a>b>c>d>eB.a<b 2020-12-22 …