早教吧作业答案频道 -->数学-->
某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区M(如图所示),M是OA上一点,M与BC相切
题目详情
某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区 M(如图所示),M是OA上一点, M与BC相切,观景台的两端A、O到 M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=
.
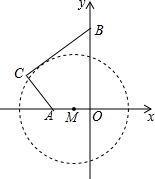
(1)求栈道BC的长度;
(2)当点M位于何处时,可以使该圆形保护区的面积最大?
| 4 |
| 3 |

(1)求栈道BC的长度;
(2)当点M位于何处时,可以使该圆形保护区的面积最大?
▼优质解答
答案和解析
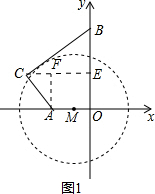 (1)如图1,过C点作CE⊥OB于E,过A作AF⊥CE于F,
(1)如图1,过C点作CE⊥OB于E,过A作AF⊥CE于F,
∵∠ACB=90°∠BEC=90°,
∴∠ACF=∠CBE,
∴tan∠ACF=tan∠OBC=
,
设AF=4x,则CF=3x,
∵∠AOE=∠AFE=∠OEF=90°,
∴OE=AF=4x,EF=OA=60,
∴CE=3x+60,
∵tan∠OBC=
.
∴BE=
CE=
x+45,
∴OB=OE+BE=4x+
x+45,
∴4x+
x+45=170,
解得:x=20,
∴CE=120(米),BE=90(米),
∴BC=
=150(米).
(2)如图2,设BC与 M相切于Q,延长QM交直线BO于P,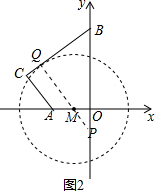
∵∠POM=∠PQB=90°,
∴∠PMO=∠CBO,
∴tan∠OBC=
.
∴tan∠PMO=
.
设OM=x,则OP=
x,PM=
x,
∴PB=
x+170,
在RT△PQB中,tan∠PBQ=
=
.
∴
=
,
∴PQ=
(
x+170)=
x+136,
设 M的半径为R,
∴R=MQ=
x+136-
x=136-
x,
∵A、O到 M上任意一点的距离均不小于80米,
∴R-AM≥80,R-OM≥80,
∴136-
x-(60-x)≥80,136-
x-x≥80,
解得:10≤x≤35,
∴当且仅当x=10时R取最大值,
∴OM=10米时,保护区的面积最大.
 (1)如图1,过C点作CE⊥OB于E,过A作AF⊥CE于F,
(1)如图1,过C点作CE⊥OB于E,过A作AF⊥CE于F,∵∠ACB=90°∠BEC=90°,
∴∠ACF=∠CBE,
∴tan∠ACF=tan∠OBC=
| 4 |
| 3 |
设AF=4x,则CF=3x,
∵∠AOE=∠AFE=∠OEF=90°,
∴OE=AF=4x,EF=OA=60,
∴CE=3x+60,
∵tan∠OBC=
| 4 |
| 3 |
∴BE=
| 3 |
| 4 |
| 9 |
| 4 |
∴OB=OE+BE=4x+
| 9 |
| 4 |
∴4x+
| 9 |
| 4 |
解得:x=20,
∴CE=120(米),BE=90(米),
∴BC=
| BE2+CE2 |
(2)如图2,设BC与 M相切于Q,延长QM交直线BO于P,

∵∠POM=∠PQB=90°,
∴∠PMO=∠CBO,
∴tan∠OBC=
| 4 |
| 3 |
∴tan∠PMO=
| 4 |
| 3 |
设OM=x,则OP=
| 4 |
| 3 |
| 5 |
| 3 |
∴PB=
| 4 |
| 3 |
在RT△PQB中,tan∠PBQ=
| PQ |
| BQ |
| 4 |
| 3 |
∴
| PQ |
| PB |
| 4 |
| 5 |
∴PQ=
| 4 |
| 5 |
| 4 |
| 3 |
| 16 |
| 15 |
设 M的半径为R,
∴R=MQ=
| 16 |
| 15 |
| 5 |
| 3 |
| 3 |
| 5 |
∵A、O到 M上任意一点的距离均不小于80米,
∴R-AM≥80,R-OM≥80,
∴136-
| 3 |
| 5 |
| 3 |
| 5 |
解得:10≤x≤35,
∴当且仅当x=10时R取最大值,
∴OM=10米时,保护区的面积最大.
看了 某地质公园为了方便游客,计划...的网友还看了以下:
如图,在A,B,C三镇在天然气管道MN的同侧,现要在管道MN上修建两个泵站P,如图,在A、B、C三 2020-05-14 …
车辆修理按作业范围可分为( )。A.车辆大修 B.总成大修 C.车辆中修 D.车辆小修 E.零件小修 2020-05-19 …
写出修辞手法画和地图的修辞手法远看山有色,近听水无声.春去花还在,人来鸟不惊.()高山不见一寸土, 2020-05-21 …
由于视图是虚表,因此对视图的修改,最终要转换为对 【】 的修改。 2020-05-23 …
在SQL中,由于对视图的修改最终要转换为对基本表的修改,因此下列只有哪种视图是可以修改的?A.行列 2020-05-23 …
在下列关于视图的叙述中,正确的一条是()。A.当修改某一视图时,导出该视图的基本表也随之被修改B. 2020-05-24 …
灌水率图的修正时,提前或推迟灌水日期不得超过( )A.1dB.2dC.3dD.4d 2020-05-28 …
灌水率图的修正时,改变灌水定额,灌水定额的调整值不应超过原定额的()A.5%B.10%C.15%D. 2020-05-28 …
灌水率图的修正,可以提前或推后灌水时间,提前或推迟灌水日期不得超过 2020-05-28 …
灌水率图的修正时,延长或缩短灌水时间与原定时间相差不应超过( )A.15%B.20%C.25%D.3 2020-05-28 …