早教吧作业答案频道 -->数学-->
如图1,△ABC和△ADE都是等边三角形.(1)求证:BD=CE;(2)如图2,若BD的中点为P,CE的中点为Q,请判断△APQ的形状,并说明理由.
题目详情
如图1,△ABC和△ADE都是等边三角形.
(1)求证:BD=CE;
(2)如图2,若BD的中点为P,CE的中点为Q,请判断△APQ的形状,并说明理由.
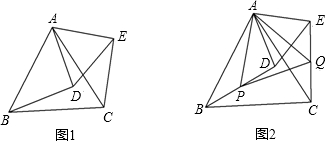
(1)求证:BD=CE;
(2)如图2,若BD的中点为P,CE的中点为Q,请判断△APQ的形状,并说明理由.

▼优质解答
答案和解析
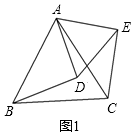 (1)∵△ABC和△ADE都是等边三角形,
(1)∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)△APQ是等边三角形.
理由:∵P是BD中点,Q是CE中点,BD=CE,
∴BP=CQ.
由(1)可得,△ABD≌△ACE,
∴∠ABP=∠ACQ,
在△ABP与△ACQ中,
,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ,
∴∠BAP+∠CAP=∠CAQ+∠CAP,
∴∠PAQ=∠BAC=60°,
∴△APQ是等边三角形.
 (1)∵△ABC和△ADE都是等边三角形,
(1)∵△ABC和△ADE都是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△ABD与△ACE中,
|
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)△APQ是等边三角形.
理由:∵P是BD中点,Q是CE中点,BD=CE,

∴BP=CQ.
由(1)可得,△ABD≌△ACE,
∴∠ABP=∠ACQ,
在△ABP与△ACQ中,
|
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ,
∴∠BAP+∠CAP=∠CAQ+∠CAP,
∴∠PAQ=∠BAC=60°,
∴△APQ是等边三角形.
看了 如图1,△ABC和△ADE都...的网友还看了以下:
商品的价格A.经常和价值不一致,不能反映价值B.是由买卖双方的讨价还价能力决定的C.能灵活反映供求 2020-05-13 …
(1)将一只蚂蚁涂上另一窝蚂蚁的气味,然后放回巢内,却被本巢内的兵蚁咬死,试分析原因..(2)一窝 2020-05-16 …
下列关于宗教崇拜对象演变的叙述,正确的是[]A.逐渐由自然神转化为人格化的民族神B.逐渐由多神崇拜 2020-05-17 …
下列的排序不正确的是()A.晶体熔点由低到高:CF4<CCl4<CBr4<CI4B.沸点由高到低: 2020-05-17 …
根据要求完成下列各题.为了引导同学们由“被动学习”转向“主动学习”,学校准备开展以“学会主动学习” 2020-06-10 …
根据质量守恒定律,回答下列问题.Ⅰ.为验证质量守恒定律,某同学设计了如图甲实验.(1)该实验的现象 2020-06-13 …
一个数(0除外)乘小数,积一定比这个数小..理由:.(判断对错,并说明理由) 2020-06-15 …
(多选)解剖环毛蚓,下列的做法正确的是()A.可以只解剖蚯蚓的前半部分而舍弃后半部分B.为了更好地 2020-07-03 …
用吸管吸取一些红墨水,把红墨水慢慢的滴在鱼口的前方,观察墨汁的流动情况是()A.墨水由鱼的口流入腮 2020-07-05 …
已知:如图,点D、E分别为△ABC的边AB、AC的中点,将△ADE绕点D旋转180°至△BDF.( 2020-07-07 …