早教吧作业答案频道 -->数学-->
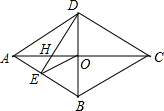
如图,四边形ABCD是菱形,对角线AC与BD相交于点O.DE⊥AB于点E.连接OE.(1)求证:∠OED=∠ACD;(2)若AC=8,DB=6,求DH的长.
题目详情
如图,四边形ABCD是菱形,对角线AC与BD相交于点O.DE⊥AB于点E.连接OE.
(1)求证:∠OED=∠ACD;
(2)若AC=8,DB=6,求DH的长.

(1)求证:∠OED=∠ACD;
(2)若AC=8,DB=6,求DH的长.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,AD=CD,
∴∠DAC=∠ACD,
∵DE⊥AB,
∴∠AOD=∠AED=90°,
∴点A,E,O,D共圆,
∵∠OED=∠CAD,
∴∠OED=∠ACD;
(2)∵四边形ABCD是菱形,AC=8,DB=6,
∴OA=
AC=4,OB=
DB=3,
∴AB=
=5,
∵S菱形ABCD=
AC•BD=AB•DE,
∴DE=
=
;
∴AE=
=
,
∵∠AEH=∠AOB=90°,∠EAH=∠OAB,
∴△AEH∽△AOB,
∴AE:AO=EH:OB,
∴
:4=EH:3,
解得:EH=
,
∴DH=DE-EH=
.
∴AC⊥BD,AD=CD,
∴∠DAC=∠ACD,
∵DE⊥AB,
∴∠AOD=∠AED=90°,
∴点A,E,O,D共圆,
∵∠OED=∠CAD,
∴∠OED=∠ACD;
(2)∵四边形ABCD是菱形,AC=8,DB=6,
∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| OA2+OB2 |
∵S菱形ABCD=
| 1 |
| 2 |
∴DE=
| ||
| AB |
| 24 |
| 5 |
∴AE=
| AD2-DE2 |
| 7 |
| 5 |
∵∠AEH=∠AOB=90°,∠EAH=∠OAB,
∴△AEH∽△AOB,
∴AE:AO=EH:OB,
∴
| 7 |
| 5 |
解得:EH=
| 21 |
| 20 |
∴DH=DE-EH=
| 15 |
| 4 |
看了 如图,四边形ABCD是菱形,...的网友还看了以下:
加点字的读音全对的一组是()A.滂(páng)沱酗(xù)酒场(chǎng)所枢(shū)纽B.逮 2020-06-28 …
下列各项中字音不正确的一项是:()A.消(xiāo)灭不屑(xiè)娇(jiāo)惯B.骄(jiā 2020-06-28 …
选出下列注音有误的一项A.悠邈(miǎo)惆怅(chóu)渗浸(shèn)打夯(hāng)B.无垠 2020-07-02 …
下列各项中字音不正确的一项是:()A.涕(tì)泪梯(tī)子府第(dì)B.饿莩(fú)俘(fú 2020-07-12 …
下列词语中加点字的读音全对的一组是()A.乾坤(qián)商榷(què)扁舟(biǎn)渌水(lǜ 2020-07-15 …
下列各项中字音不正确的一项是:()A.谗(Chán)邪剽(piāo)掠锱(zī)铢B.口谕(yù)迤 2020-11-07 …
下列词语中加点字的注音,全都正确的一组是()A.稼穑(sè)同胞(pāo)宽宥(yòu)堤(dī)坝 2020-11-08 …
下列各项中字音不正确的一项是:()A.暴虐(nüè)怅寥廓(chàng)峥嵘(róng)B.遒劲(q 2020-12-23 …
在低于O℃的气温下,有一个深水湖泊的表面结了厚厚的一层冰,冰层下面是水.下面的说法中错误的是A.冰的 2020-12-24 …
A.真谛(dì)疟疾(yuè)狭隘(ài)骇人听闻(hài)B.剖开(pōu)纤维(xiān)峰巅( 2021-01-17 …