早教吧作业答案频道 -->数学-->
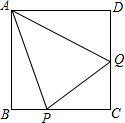
如图,正方形ABCD的边长为1,P、Q分别为边BC、CD上的点,连接PQ,若△CPQ的周长是2,求∠PAQ的度数.
题目详情
如图,正方形ABCD的边长为1,P、Q分别为边BC、CD上的点,连接PQ,若△CPQ的周长是2,求∠PAQ的度数.

▼优质解答
答案和解析
如图,延长CB使得BH=DQ,连接AH.
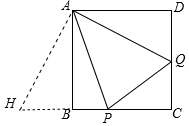
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABH=90°,
在△ADC和△ABH中,
,
∴△ADQ≌△ABH,
∴∠DAQ=∠BAH,AQ=AH,
∵PC+CQ+PQ=2,CP+PB+CQ+QD=2,
∴PQ=PB+DQ=PB+BH=PH,
在△APH和△APQ中,
,
∴△APH≌△APQ,
∴∠PAH=∠PAQ,
∵∠PAH=∠PAB+∠BAH=∠PAB+∠DAQ,
∴∠PAQ=∠PAB+∠DAQ,∵∠BAD=90°,
∴∠PAQ=
∠BAD=45°.

∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABH=90°,
在△ADC和△ABH中,
|
∴△ADQ≌△ABH,
∴∠DAQ=∠BAH,AQ=AH,
∵PC+CQ+PQ=2,CP+PB+CQ+QD=2,
∴PQ=PB+DQ=PB+BH=PH,
在△APH和△APQ中,
|
∴△APH≌△APQ,
∴∠PAH=∠PAQ,
∵∠PAH=∠PAB+∠BAH=∠PAB+∠DAQ,
∴∠PAQ=∠PAB+∠DAQ,∵∠BAD=90°,
∴∠PAQ=
| 1 |
| 2 |
看了 如图,正方形ABCD的边长为...的网友还看了以下:
已知光由折射率为2为的玻璃射向真空,如图所示的四个图中,其光路图正确的是()A.B.C.D. 2020-05-02 …
log以2为底8*log以2为底4系咪可以变成log以2为底8+log以2为底4定系8直接*4然后 2020-05-13 …
3个化学离子=氯酸根离子高锰酸根离子锰酸根离子怎么表达?(例如SO4/2-)这样表达吧,起码我看的 2020-05-14 …
电表接2.5的线到空气开关然后再从空气开关接6平方的线到楼上家里空气开关可以不可以 2020-05-16 …
电压表与电流表接口为什么不同电压表接1,2电流表接1,3电压表接线A,B电流表接线A,C为什么不都 2020-05-17 …
《读者》上一篇关于一个哲学家将自己在家中的文章?整篇文章讲得就是他呆在郊外,不与他人接触,为的是自 2020-05-23 …
做几道直接引语变间接引语的英语题1.MrWangsaid,“Iwillleaveforshangh 2020-06-03 …
一个电阻为600Ω,电感为2.55H的线圈接在工频电压为380V的交流电源上,1)及各元件电压的有 2020-06-03 …
开关柜基础型钢安装完毕后,需可靠接地,配电室内接地线应与基础型钢焊接,且不少于2处,焊接面为 2020-06-07 …
将一电阻接在电动势为6V,内阻为2欧的电源上,若该电阻消耗的电功率为4W,则此时流过该电阻的电流为 2020-06-09 …